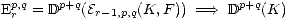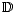1. Introduction
We construct a series of spectral sequences for the hypercohomology of a filtered
complex. The basic constructions used are the shift (dècalée) operation of Deligne and its
inverse [3].
Theorem 1.1. Let D : C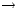 C' be a left exact functor between abelian categories.
Assume that C has enough injectives. For any good filtered complex (K,F) of objects
in C we have natural spectral sequences for each r > 1.
C' be a left exact functor between abelian categories.
Assume that C has enough injectives. For any good filtered complex (K,F) of objects
in C we have natural spectral sequences for each r > 1.
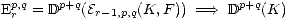
For r = 1 this coincides with the spectral sequence for the hypercohomology of
a filtered complex ([3]; section 1.4.5). For r = 2 and the trivial filtration F this
coincides with the Leray spectral sequence for hypercohomology (see [3]; section
1.4.7).
Here 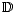 i’s denote the hyperderived functors associated with D and Er-1,p,q denotes the
complex of Er-1 terms of the spectral sequence (see [3] section 1.3.1) for a filtered
complex which contains Erp,q as the (p + q)-th term.
i’s denote the hyperderived functors associated with D and Er-1,p,q denotes the
complex of Er-1 terms of the spectral sequence (see [3] section 1.3.1) for a filtered
complex which contains Erp,q as the (p + q)-th term.
As applications, we provide proofs of some facts which are apparently well
known to experts but are not well-documented in the literature (see however
[7],[4]; the proof of the latter two applications is attributed to P. Deligne in [4]
and [1]). The first is the existence of a Leray spectral sequence for de Rham
cohomology. The second is the comparison of this spectral sequence with the Leray
spectral sequence for singular cohomology. The third is the isomorphism of the
Bloch-Ogus-Gersten spectral sequence with the Leray spectral sequence from E2
onwards.
In Section 2 we recall some facts and definitions due to Deligne ([3] sections 1.3 and
1.4). In Section 3 we generalise some of these ideas to get the main results. The
applications are elementary corollaries of the lemmas from section 3 and are
proved in Section 4. In appendix A we recapitulate the required material from
[3] and in appendix B we redo the main result using the language of derived
categories.
I am grateful to V. Srinivas for advice and encouragement. I followed up his
suggestion that the problem of the Bloch-Ogus spectral sequence and that of the Leray
spectral sequence for de Rham cohomology could be related. J. Biswas and Balaji
Srinivasan have had to listen to half-baked versions of the results and also had to
correct my wrong impressions about the existence of connections for proper
submersions.
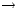 C' be a left exact functor between abelian categories.
Assume that C has enough injectives. For any good filtered complex (K,F) of objects
in C we have natural spectral sequences for each r > 1.
C' be a left exact functor between abelian categories.
Assume that C has enough injectives. For any good filtered complex (K,F) of objects
in C we have natural spectral sequences for each r > 1.