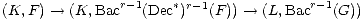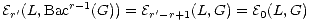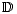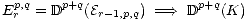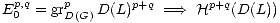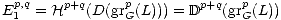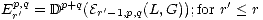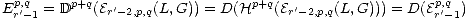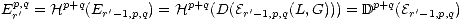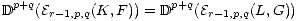3. Extensions to [3]
We now extend the definition ([3]; 1.3.6) slightly. Let us first introduce the notation
Er,p,q(K,F) for the complex of Er terms which contains the term Erp,q(K,F) at the
p + q-th position. When the integers p and q are irrelevant we will abbreviate this to
Er(K,F). Note that we have the equality of complexes Er,p,q = Er,p+r,q-r+1.
Definition 3.1. A morphism f : (K,F)  (L,G) of good filtered complexes is
said to be a level-r filtered quasi-isomorphism if the morphisms Er-1(f) induce
quasi-isomorphisms Er-1(K,F)
(L,G) of good filtered complexes is
said to be a level-r filtered quasi-isomorphism if the morphisms Er-1(f) induce
quasi-isomorphisms Er-1(K,F)  Er-1(L,G), i. e. Erp,q(f) are isomorpisms for
all integers p and q.
Er-1(L,G), i. e. Erp,q(f) are isomorpisms for
all integers p and q.
A level-1 filtered quasi-isomorphism is what was earlier (2.5) called a filtered
quasi-isomorphism.
We extend the definition ([3]; 1.4.5) in a similar way.
Definition 3.2. A level-r filtered injective resolution of a good filtered complex
(K,F) is a level-r filtered quasi-isomorphism (K,F)  (L,G) such that the terms
Er'p,q(L,G) are injective for all r' < r and all integers p and q.
(L,G) such that the terms
Er'p,q(L,G) are injective for all r' < r and all integers p and q.
A similar definition can be given with the property injective replaced by the property
D-acyclic in the context of a left-exact functor C  C' as before. A level-1
filtered injective resolution is what was earlier (2.6) called a filtered injective
resolution.
C' as before. A level-1
filtered injective resolution is what was earlier (2.6) called a filtered injective
resolution.
Example 3.3. Let K be any complex on objects in C. We put the trivial filtration
F on K by defining F0K = K and F1K = 0. Then we note as in ([3]; 1.4.6) that
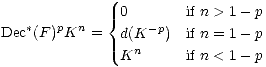
Thus, grDec *(F)pK is the complex concentrated in degrees -p and 1 - p.
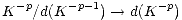
There is a natural morphism to this from the single term complex H-p(K)
concentrated in degree -p which is clearly a quasi-isomorphism.
Fact 3.4. Let L denote the total complex of a Cartan-Eilenberg resolution [2] I
of K. Let Gp(L) be the total complex of the subcomplex I>p. Let F be the trivial
filtration on K. Then the natural morphism (K,F)  (L,G) is a level-2 filtered
injective resolution.
(L,G) is a level-2 filtered
injective resolution.
Proof. As noted above we have
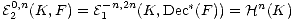
and the remaining E2 terms are 0. We have the identity E0p,n(J,G) = Ip,n and so
we deduce E1p,n(J,G) = Hn(Ip). Since I is a Cartan-Eilenberg resolution these E1
terms give an injective resolution of Hn(K). Thus we have the result. ![[]](msam10-3.png)
We use the fact (2.7) to prove
Lemma 3.5. If C has sufficiently many injectives then any good filtered complex
(K,F) has a level-r injective resolution for any r > 1.
Proof. Let (K,(Dec*)r-1(F))  (L,G) be a (level-1) filtered injective resolution
(which exists by (2.7)). Consider the composite morphism
(L,G) be a (level-1) filtered injective resolution
(which exists by (2.7)). Consider the composite morphism
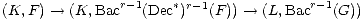
By (3) we see that the first morphism is a level-r quasi-isomorphism. Also by (1) we
see that the second morphism is a level-r quasi-isomorphism. Hence the composite
is also a level-r quasi-isomorphism. Now by (1) and (2.3) we have for r' < r
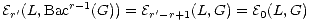
By assumption the latter terms are injective. ![[]](msam10-3.png)
Next we note the naturality of such a resolution.
Lemma 3.6. Suppose (K,F) is a good filtered complex such that Er'p,q(K,F) are
injective for all r' < r and all integers p and q. Let f : (K,F)  (L,G) be a
level-r injective resolution then there is a morphism g : (L,G)
(L,G) be a
level-r injective resolution then there is a morphism g : (L,G)  (K,F) such that
Er-1(f o g) and Er-1(g o f) are homotopic to identity.
(K,F) such that
Er-1(f o g) and Er-1(g o f) are homotopic to identity.
Proof. Note that Er-1(f) : Er-1(K,F)  Er-1(L,G) is a quasi-isomorphism of
complexes of injectives. Hence there is a morphism gr-1 : Er-1(L,G)
Er-1(L,G) is a quasi-isomorphism of
complexes of injectives. Hence there is a morphism gr-1 : Er-1(L,G)  Er-1(K,F)
such that Er-1(f)ogr-1 and gr-1oEr-1(f) are homotopic to identity. By induction
we assume that we are given the morphism gr' : Er'(L,G)
Er-1(K,F)
such that Er-1(f)ogr-1 and gr-1oEr-1(f) are homotopic to identity. By induction
we assume that we are given the morphism gr' : Er'(L,G)  Er'(K,F). We wish to
find a morphism gr'-1 : Er'-1(L,G)
Er'(K,F). We wish to
find a morphism gr'-1 : Er'-1(L,G)  Er'-1(K,F) such that it induces gr' on the
cohomology of the Er'-1 terms (which is Er'). This is possible since the Er'-1,p,q’s
are bounded below complexes of injectives. Thus we obtain g0,p : grGpL
Er'-1(K,F) such that it induces gr' on the
cohomology of the Er'-1 terms (which is Er'). This is possible since the Er'-1,p,q’s
are bounded below complexes of injectives. Thus we obtain g0,p : grGpL  grFpK.
Again we have that K and L are bounded below complexes of injectives and so we
obtain the required morphism g which satisfies grp(g) = g0,p.
grFpK.
Again we have that K and L are bounded below complexes of injectives and so we
obtain the required morphism g which satisfies grp(g) = g0,p. ![[]](msam10-3.png)
We have the following modification of ([3]; 1.4.5):
Lemma 3.7. Let D : C C' be a left-exact functor and assume that C has enough
injectives. Let
C' be a left-exact functor and assume that C has enough
injectives. Let 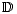 i denote the associated hypercohomology functors and let (K,F) be
a good filtered complex in C. Then for any r > 1 we have a natural spectral sequence
i denote the associated hypercohomology functors and let (K,F) be
a good filtered complex in C. Then for any r > 1 we have a natural spectral sequence
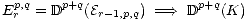
Proof. Let (K,F)  (L,G) be a level-r filtered D-acyclic resolution (for example
we can take a level-r filtered injective resolution by lemma (3.5)). Consider the
good filtered complex (D(L),D(G)) in C'. The associated spectral sequence is
(L,G) be a level-r filtered D-acyclic resolution (for example
we can take a level-r filtered injective resolution by lemma (3.5)). Consider the
good filtered complex (D(L),D(G)) in C'. The associated spectral sequence is
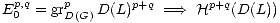
Now, by (2.8) the latter term is 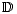 p+q(K). Since grGp(Ln) are D-acyclic for
all integers p and n and the filtrations are finite, we see that grD(G)p(D(L)) =
D(grGp(L)).
p+q(K). Since grGp(Ln) are D-acyclic for
all integers p and n and the filtrations are finite, we see that grD(G)p(D(L)) =
D(grGp(L)).
Now by definition Elp,q = Hp+q(El-1,p,q). Thus we obtain
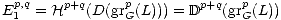
since grGp(Ln) are D-acyclic. We now claim by induction that
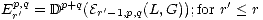
Assume this for r'- 1. Now since r'- 1 < r we have Er'-1(L,G) consists of
D-acyclics. Thus we see by (2.9) that
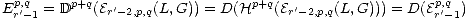
But then by definition of 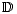 i’s we have
i’s we have
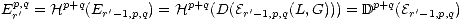
This proves the claim by induction.
Now we have Er-1,p,q(K,F)  Er-1,p,q(L,G) is an D-acyclic resolution. Thus
Er-1,p,q(L,G) is an D-acyclic resolution. Thus
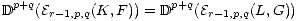
Hence we obtain the required spectral sequence. The naturality of this spectral
sequence easily follows from the lemma (3.6) by the usual techniques. ![[]](msam10-3.png)
Now we note that for r = 1 this spectral sequence is exactly the one constructed by
Deligne in ([3];1.4.5). For r = 2 we see that this is the Leray spectral sequence for
hypercohomology by applying the level-2 injective resolution given by Cartan-Eilenberg
(3.4). From the above proof we see that we obtain our “new” spectral sequence. On the
other hand the E2 spectral sequence associated with the Cartan-Eilenberg resolution is
precisely what is called the Leray spectral sequence for hypercohomology. This completes
the proof of the main theorem (1.1).
 (L,G) of good filtered complexes is
said to be a level-r filtered quasi-isomorphism if the morphisms Er-1(f) induce
quasi-isomorphisms Er-1(K,F)
(L,G) of good filtered complexes is
said to be a level-r filtered quasi-isomorphism if the morphisms Er-1(f) induce
quasi-isomorphisms Er-1(K,F)  Er-1(L,G), i. e. Erp,q(f) are isomorpisms for
all integers p and q.
Er-1(L,G), i. e. Erp,q(f) are isomorpisms for
all integers p and q.
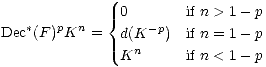
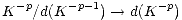
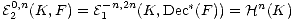
![[]](msam10-3.png)