Fact 2.2 ([3]; 1.3.1). For any good filtered complex (K,F) there is a spectral sequence
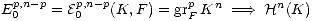
such that the filtration induced by this spectral sequence on Hn(K) is the same as that induced by F.
We recall some facts proved by Deligne in ([3]; 1.3 and 1.4) with slightly different notations. The details can also be found in the appendix A. Let C be an abelian category. All objects, morphisms, etc. will be with reference to this category.
Definition 2.1. We say (K,F) is good filtered complex in C if K is a co-chain complex in C which is bounded below and F is a filtration on it which is compatible with the differential and is finite on Kn for each integer n.
We will always work with good filtered complexes in this paper. For any co-chain complex K let Hn(K) denote its n-th cohomology.
Fact 2.2 ([3]; 1.3.1). For any good filtered complex (K,F) there is a spectral sequence
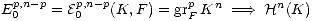
such that the filtration induced by this spectral sequence on Hn(K) is the same as that induced by F.
Fact 2.3. The definitions of Erp,q(K,F) given in (loc. cit. ) make sense for all integers r (not only positive integers r). The equalities Erp,q = E0p,q for r < 0 hold and the differentials dr are 0 for r < 0 due the compatibility of the filtration F with the differential on K.
Next Deligne defines various shifted filtrations associated with the given one. First of all we define ([3]; proof of 1.3.4)
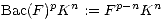
Deligne shows that (loc. cit. ),
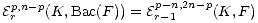
for all integers r. By induction on l we obtain
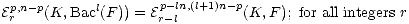 | (1) |
Moreover, Deligne notes the following fact about renumbering spectral sequences (actually he only notes it for s-r=1).
Fact 2.4. Let Eap,q be the terms of a spectral sequence which starts at a = r, then we can obtain another spectral sequence E'bp,q starting at the term b = s by setting
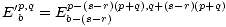
Next we consider the dual shifted filtration ([3]; section 1.3.5),
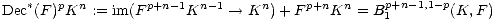
Deligne shows (loc. cit. ) that
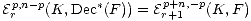
for all r > 1. By induction on l we obtain
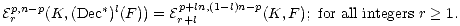 | (2) |
Combining the results for Bac and Dec we see that
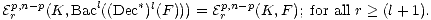 | (3) |
Definition 2.5 ([3]; 1.3.6). A morphism f : (K,F)  (L,G) of good filtered
complexes is said to be a filtered quasi-isomorphism if the morphisms grp(f) :
grFp(K)
(L,G) of good filtered
complexes is said to be a filtered quasi-isomorphism if the morphisms grp(f) :
grFp(K)  grGp(L) is a quasi-isomorphism, i. e. E1p,q(f) are isomorpisms for all
integers p and q.
grGp(L) is a quasi-isomorphism, i. e. E1p,q(f) are isomorpisms for all
integers p and q.
Definition 2.6 ([3]; 1.4.5). A filtered injective resolution of a good filtered
complex (K,F) is a filtered quasi-isomorphism (K,F)  (L,G) such that the terms
grLpGn are injective for all integers p and n.
(L,G) such that the terms
grLpGn are injective for all integers p and n.
A similar definition can be given with the property injective replaced by the
property D-acyclic in the context of a left-exact functor D : C C' as in ([3];
1.4.1).
C' as in ([3];
1.4.1).
The following well-known fact is used in ([3]; 1.4.5)
Fact 2.7. If C has sufficiently many injectives then any good filtered complex (K,F) has a filtered injective resolution.
If D : C C' is a left-exact functor and C has enough injectives, then we have the
hypercohomologies
C' is a left-exact functor and C has enough injectives, then we have the
hypercohomologies 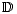 i(K) in C' associated with any bounded below cochain complex
K
i(K) in C' associated with any bounded below cochain complex
K
Fact 2.8 ([3]; 1.4.4). The 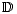 i(K) are computed as the cohomologies of the complex
D(L) for any quasi-isomorphism K
i(K) are computed as the cohomologies of the complex
D(L) for any quasi-isomorphism K  L where the terms of L are D-acyclic.
L where the terms of L are D-acyclic.
We will also need the following well-known fact.