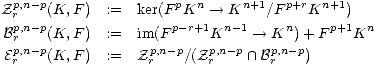
We reproduce some facts proved by Deligne in ([3]; 1.3 and 1.4) with slightly different notations. Let (K,F) be a filtered co-chain complex which is bounded below and such that the filtration is finite on each term of the complex. Moreover, we assume that the differential on K is compatible with the filtration. We define for each integer r,
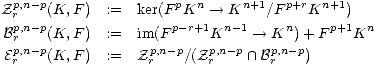
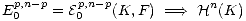
such that the filtration induced by this spectral sequence on Hn(K) is the same as that induced by F.
Next we define various shifted filtrations associated with the given one. First of all we define
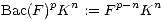
One then computes that for all integers r,
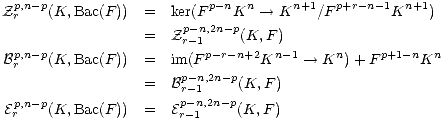
Next we consider the dual shifted filtration,
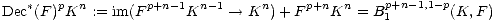
One computes the following equations for all r > 0,
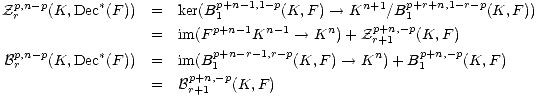
 Br+1p+n,-p. Hence one deduces that
Br+1p+n,-p. Hence one deduces that
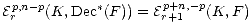
for all r > 1.