[next] [tail] [up]

1. Special divisors and a conjecture of M. Green

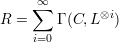
Let C be a projective algebraic curve of genus g ≥ 2 over a field k and L be any line bundle on C that is generated at stalks by its space of global sections. We then consider

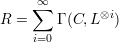
∞ R = ∑ Γ (C,L ⊗i) i=0

the homogeneous coordinate ring of C with respect to L. Then, we may write a minimal free resolution of R as a graded module over S, the Symmetric algebra on Γ(C,L),

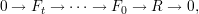
0 → Ft → ⋅⋅⋅ → F0 → R → 0,

where

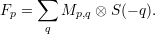
∑ Fp = Mp,q ⊗ S(- q). q

H. H. Martens [15] has defined the Clifford Index γC of C as the minimum of deg(D) - 2dim∣ D where D runs over all divisors on C such that h0(C,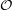OC(D)) > 1 and h1(C,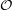OC(D)) > 1. We are concerned with the following

Conjecture 1.1 (M. Green). With notation as above, Mp,p+q = 0, for all p,q such that q > 1 and p ≤ γC - (deg(L )- 2dim |L).

Let EL be the vector bundle on C defined by the following natural exact sequence,

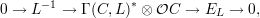
0 → L-1 → Γ (C,L)* ⊗ OC → EL → 0,

and V = Γ(C,L)*. Then it is easily seen that,

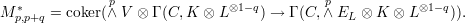
M * = coker(p∧ V ⊗ Γ (C, K ⊗ L ⊗1-q) → Γ (C,∧pE ⊗ K ⊗ L ⊗1-q)). p,p+q L

Thus, the conjecture of Green is equivalent to the surjectivity of this morphism for p,q in the given range. In Chapter 1 of the thesis we show

Theorem 1.2. Let C be an projective algebraic curve of genus g ≥ 2 over a field k, and L a line bundle on it that is generated at stalks by its space V = Γ(C,L)* of global sections. Further, let EL be the vector bundle on C defined by the natural exact sequence

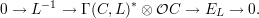
-1 * 0 → L → Γ (C,L) ⊗ OC → EL → 0.

Then, the image of

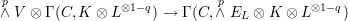
p ⊗1-q p ⊗1-q ∧ V ⊗ Γ (C,K ⊗ L ) → Γ (C, ∧ EL ⊗ K ⊗ L )

contains all locally decomposable sections, whenever q > 1 and

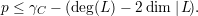
p ≤ γC - (deg(L )- 2dim |L).

As a result of this work the conjecture of M. Green now follows from

Conjecture 1.3. Let EL be the ample vector bundle on a curve C as above Then the locally decomposable sections of 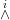∧iEL span the vector space of all sections, for all i.

In a later paper (see 5) we have proved this conjecture in some cases. Even for a general ample bundle E which is generated by its space of global sections we know of no situation contrary to this conjecture.

[next] [front] [up]