Conjecture 5.1. The vector bundle EK is such that the sections of 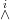 EK
are spanned by the decomposable sections.
EK
are spanned by the decomposable sections.
In collaboration with K. Hulek and S. Ramanan we have explored a conjecture made along with S. Ramanan on the syzygies of canonical curves. Specifically, we have conjectured that (with notation as in 1)
Conjecture 5.1. The vector bundle EK is such that the sections of 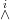 EK
are spanned by the decomposable sections.
EK
are spanned by the decomposable sections.
This conjecture implies the conjecture of M. Green mentioned in 1.
In this work we have proved this conjecture for trigonal curves and also for plane quintics. This covers the case of Clifford Index 1. The case of hyperelliptic curves (Clifford Index 0) is elementary.