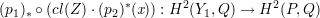2. Kuga-Satake varieties and K3 surfaces
Given a K3 surface, M. Kuga and I. Satake [13] associate to it an abelian
variety. P. Deligne [5] has constructed an absolute Hodge cycle on the product
of the abelian variety and the K3 surface. When the K3 surface is the
desingularisation of a double cover of the plane branched along six lines in
general position, the abelian variety is isogenous to the product of a
number of copies of a four dimensional abelian variety. We construct the
Kuga-Satake-Deligne correspondence between this four dimensional abelian
variety and the K3 surface in this case.
More precisely, we prove
Theorem 2.1. Let Y 1 be the desingularisation of the double cover of the
plane branched along six lines in general position. Then there is an abelian
variety P and a codimension two algebraic cycle on P × Y 1 such that the
homomorphism
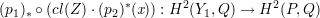
is an inclusion when restricted to the lattice of transcendental cycles of Y 1,
and hence this cycle represents the Kuga-Satake-Deligne correspondence.
This result settles affirmatively a special case of the Hodge conjecture.