Problem 3.1. Suppose G is a semi-simple algebraic group over C, P ⊂ G
a maximal parabolic subgroup, Y = G∕P. Let f : Y → X be a finite,
surjective morphism of degree > 1 to a smooth variety X; then is X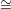 Pn ?
(n = dimX = dimY )
Pn ?
(n = dimX = dimY )
This work (done jointly with V. Srinivas) arose out of an attempt to understand the following problem of Lazarsfeld [14]:
Problem 3.1. Suppose G is a semi-simple algebraic group over C, P ⊂ G
a maximal parabolic subgroup, Y = G∕P. Let f : Y → X be a finite,
surjective morphism of degree > 1 to a smooth variety X; then is X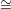 Pn ?
(n = dimX = dimY )
Pn ?
(n = dimX = dimY )
Lazarsfeld (loc. cit.) answers this in the affirmative when Y = Pn, using the proof by S. Mori [16] of Hartshorne’s conjecture. The general case seems to be open even for Grassmann varieties.
We show that:
if Y = G∕P is as above and f : Y → Y is a finite self map
of degree > 1, then Y 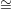 Pn.
Pn.
More generally, we prove the following:
Theorem 3.2. Let G be a simply connected, semi-simple algebraic group over C. Let P ⊂ G be a parabolic subgroup, and let Y = G∕P be the homogeneous space. Let f : Y → Y be a generically finite morphism. Then there exist parabolic subgroups P0,P1,…,Pm of G containing P, and a permutation σ of {1,2,…,m} such that:
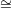 Pni for i ≥ 1, for some integers
ni > 0, such that nσ(i) = ni for all i.
Pni for i ≥ 1, for some integers
ni > 0, such that nσ(i) = ni for all i.
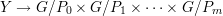
is an isomorphism, under which f : Y → Y corresponds to the
product f0 × f1 × × fm, where f0 : G∕P0 → G∕P0 is an
isomorphism and fi the composite
× fm, where f0 : G∕P0 → G∕P0 is an
isomorphism and fi the composite
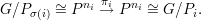
Next, we prove
Theorem 3.3. Problem 1 has an affirmative answer if Y is a smooth quadric hypersurface of dimension ≥ 3.
Remark: This includes the case of the Grassmannian Y = G(2,4).
We also show:
Proposition 3.4. Let k ≤ n,2 ≤ l ≤ m be integers, such that there exists a finite surjective morphism between Grassmann varieties
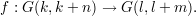
Then k = l,m = n and f is an isomorphism.
In contrast with the above algebraic results, we can construct topological maps of degree greater than one in the following cases: