2 The axiomatic approach

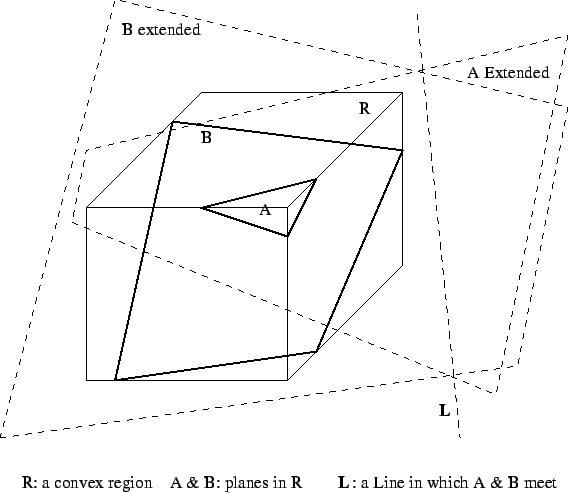
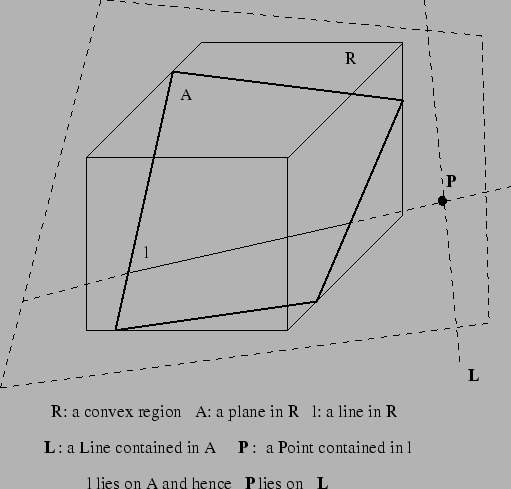
In order to avoid the many choices for the axiom of parallels we look at those axioms that are satisfied by a convex region of space (see Figure 1) in any axiomatic geometry--Euclidean or not. The basic undefined entities are points, lines and planes and the undefined relations among them are incidence (to-lie-on) and separation (between-ness). The entities and relations are made clear by the following axioms.

Figure 1: The geometry of a convex region

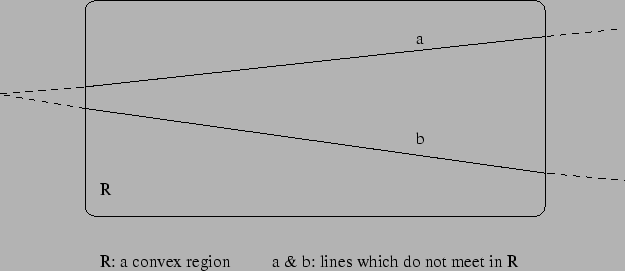We begin with the axioms of incidence:

1. Any two points lie on exactly one line and any line has at least two points on it.
2. Any three points not all on one line lie on exactly one plane and any plane has at least three non-collinear points on it.
3. If two points of a line are on a plane then every point of the line is on the plane (we then say that the line is on the plane).

Then we have the axioms of dimension:

1. There are at least four points which are non-collinear and non-coplanar.
2. If two planes meet then they meet in at least a pair of points.

The axioms of order and separation:

1. If a point B is between the points A and C then A, B, C are collinear and B is between C and A.
2. If A, B, C are distinct collinear points then exactly one is between the other two.
3. If A and B are distinct points there is at least one point C so that B is between A and C and a point D so that D is between A and B.
4. If A, B, C are non-collinear points and l is a line in the plane of A, B, C so that none of these points lie on l, then if l contains a point between A and B then it must contain a point between A and C or a point between B and C.

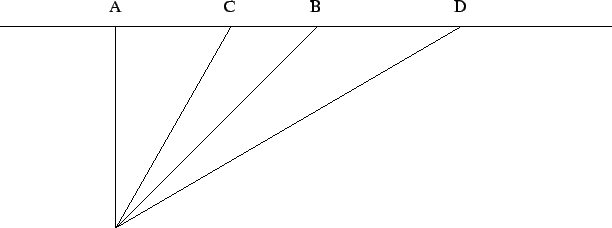
Of these the last axiom is rather special and is called Pasch's axiom (see Figure 2). We shall see later that this is the one property characterising planes in axiomatic geometry which shows that there are no planes in general Riemannian geometry.

Figure 2: Pasch's axiom of separation

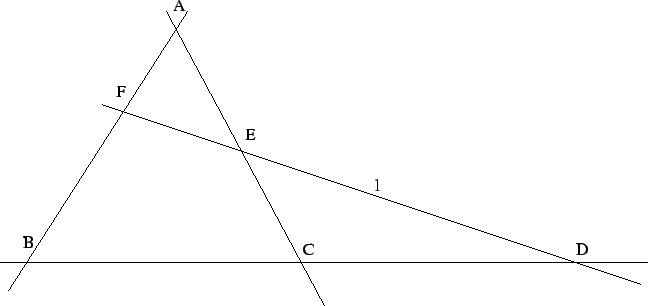Finally, we have the Archimedean least upper bound principle which gives us the least upper bound property for points on a line:

Given a sequence of points A_n and a point B such that A_{n + 1} is between B and A_n for all n, there is a point C such that C is between B and A_n for all n and for all points D lying between B and A_n for all n, D is between B and C.

Figure 3: Archimedean least upper bound principle

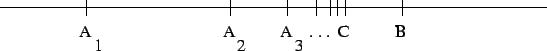A much briefer list of equivalent axioms was provided by Veblen using only the notion of points and the relation of between-ness; we use the symbol [ABC] to denote B lies between A and C.

1.

There are at least two distinct points.

2.

For any two distinct points A and B there is a point C so that [ABC].

3.

If [ABC] then A, B and C are distinct.

4.

If [ABC] then [CBA] but not [BCA].

Defn.

We say that C lies on the line l (AB) if C = A or C = B or [ABC] or [ACB] or [CAB]. A pair of lines is said to meet if they have a point in common. If A, B, C all lie on a line we say that they are collinear.

5.

If C and D are distinct points on the line l (A, B) then A lies on l (C, D).

6.

There is at least one point not on l (A, B).

7.

If A, B, C are non-collinear and D,E are points so that [BCD] and [AEC] then there is a point F so that [AFB] and F lies on the line l (D, E).

Defn.

If A, B, C are non-collinear points then a point D is said to be coplanar with A, B, C if it lies on a line which meets two out of the three lines l (A, B), l (B, C), l (A, C). The locus of all such points is called the plane determined by the three non-collinear points A, B, C.

8.

There is at least one point not on the plane determined by three non-collinear points A, B, C.

9.

Any two planes which meet have at least two distinct points in common.

10.

Let the points of a line be divided into two disjoint classes each of which satisfy: if A and B lie in the class the so does every point C such that [ACB]. Then there is a point O on the line and a pair of points P and N such that [NOP] and the two classes consists of all points between N (respectively P) and O. (In addition O lies in one of the classes.)

To check that a geometry conforms to these axioms is obviously easier than to check the same for Hilbert's axioms; but the equivalence of the two systems shows us that the former is enough.

Now we will outline how the points, lines and planes of such a geometry can be realised as the points, lines and planes of a convex region in coordinate 3-space preserving all the relations of incidence and between-ness; that is to say we have an embedding of our geometry into that of coordinate 3-space.

The first step is to construct a geometry consisting of ``ideal'' points, lines and planes; these would have ``existed'' if our geometry were not confined to a region.

The collection of all lines passing through a fixed point has the following properties:

1. Any pair of lines in this collection are coplanar.
2. For every point there is a line from this collection that contains it.

Thus we define an ``ideal point'' or Point to be a collection of lines with the above two properties (see Figure 4). Any pair (L₁, L₂) of distinct coplanar lines then determines a Point constructed as follows:

1. We take any plane p₁ containing L₁ and a different plane p₂ containing L₂ which meets p₁. Then we add the line of intersection L₃ = p₁ $\cap$ p₂ to our collection.
2. Let p be the plane containing L₁ and L₂ and p' be any other plane containing a line L₃ constructed as above, such that p' meets p. We add the line of intersection L₄ = p $\cap$ p' to out collection.

We leave it to the reader to check that such a collection indeed satisfies the two properties mentioned above. Moreover, any point clearly gives us a Point as the collection of all lines containing this point.

Figure 4: A collection of lines determines a Point

Given a pair of distinct Points A and B we consider those planes which contain a line each from the collections corresponding to A and B. The collection of all these planes determine an ``ideal line'' or Line. Any pair (p₁, p₂) of distinct planes then determines a Line constructed as follows:

1. We choose a pair of planes (q₁, q₂) such that each q_i meets each p_j.
2. Let A_i be the Point determined by the pair of lines (q_i $\cap$ p₁, q_i $\cap$ p₂).
3. A plane p belongs to our collection if it contains a line in each of the collections A₁ and A₂.

We leave it to the reader to check that this construction is independent of the choice of the pair (q₁, q₂). Moreover, we also note that the collection of all planes containing a line also satisfies the required conditions and thus determines a Line.

Figure 5: A collection of planes determines a Line

We say that a Point lies on a Line if every plane that belongs to the collection determining the Line contains a line that belongs to the collection determining the Point. This specifies the notion of incidence for Points and Lines. It is clear that if a Line L is determined by the line L' then L contains the Point A if and only if L' lies in the collection corresponding to the Point A. In particular, if the Point A is that determined A', then A lies on L if and only if A' lies on L'.

Figure 6: A Line contains a Point

Thus we have embedded our given geometry into an ``ideal'' geometry of Points and Lines with relations of incidence and separation. What are the axioms satisfied by this ``ideal'' geometry? We claim that the following axioms are satisfied:

1. Any pair of Points A and B lie on exactly one Line. We denote this line by AB.
2. Given four Points A, B, C and D, the Line AB meets the Line CD if and only if the Line AD meets the Line BC. In this case we call the four Points coplanar.
3. There are five Points so that no four of these are coplanar.
4. Given any five Points A, B, C, D and E, there is a point F on the Line AB so that the Points C, D, E and F are coplanar.

The first three axioms are the axioms of incidence and the latter two are the axioms of dimension for Projective geometry of 3 dimensions. It is a well-known theorem (see for example [2]) that such a geometry is isomorphic to the coordinate Projective geometry over a skew-field (that is multiplication need not be commutative).

The relation of separation is a little more intricate. We will try to define the relation picturised in Figure 7. Given two pairs (A,B) and (C,D) of Points lying on a Line L; we say that the pairs separate each other if for some plane p in the collection L and some point O in the plane p, there is a line L' in p and four points A', B', C' and D' on L' so that:

1. The lines OA', OB', OC' and OD' are in the collections A, B, C and D respectively.
2. B' and C' are between A' and D', and B' is between A' and C'.

We use the notation AB||CD to denote this relation. Now in case the Points A, B, C and D correspond to points A', B', C' and D' respectively, then the two relations of separation coincide; AB||CD if and only these points are all collinear, and either C is between A and B while D is not or D is between A and B and C is not.

Figure: AB||CD on a Projective Line

The axioms satisfied by the relation of separation are:

1. If A, B, C and D are collinear and distinct then exactly one of the relations AB||CD, AD||BC and AC||BD holds.
2. If A, B and C are collinear then there is a Point D so that AB||CD.
3. If AB||CD and O is a Point, and L any Line so that the Points A', B', C', D' of intersection of L with the Lines OA, OB, OC and OD respectively are distinct, then A'B'||C'D' holds.
4. Given a sequence of Points A_n and Points B and O such that A_nB||A_{n + 1}O holds for all n, then there is a Point C so that A_nB||CO holds for all n; and so for all points D so that A_nB||DO holds for all n, we have CB||DO

The first three are the axioms of separation for Projective geometry and the last is a form of the Archimedean least upper bound principle. These axioms assure us that the base skew-field of our projective space geometry is a complete ordered skew-field--which is then a (commutative) field. Moreover, under some set theoretic assumptions about cardinality this is just the field of real numbers.

Thus our ``ideal'' geometry is none other than coordinate Projective geometry of of dimension 3 over the field of real numbers. Hence we have an embedding of the given geometry into real Projective space geometry.

The collection of all Points on a Line thus forms a real Projective line which cannot be totally ordered in a way so as to satisfy the Archimedean least upper bound principle. Thus for any line there is at least one Point A which lies on the corresponding Line that does not correspond to a point. Moreover, if C and D are points on the line then every Point B so that AB||CD corresponds to a point B. In other words the geometry we have is that of a convex subset of Projective space. For any such subset one can find a Projective plane that does not meet it. Thus the convex subset is actually contained in real Affine space; in other words we have a coordinatisation of our geometry.