Implicit functions

We will prove the implicit function theorem.

Let f (x, y) be a continuous function of two variables so that it is continuous, and differentiable with respect to y when x is kept fixed; in particular, we have expression

f (x, y) = f₀(x, y₀) + f₁(x, y₀)(y - y₀) + o_x(y - y₀)

where the subscript in the o_x denotes the dependence of the condition on x. The function f₁(x, y) is denoted by $\partial$f /$\partial$y and is called the partial derivative of f with respect to y (we have already seen this for the case of polynomials). We further assume that f₁ is continuous.

Figure 7: The implicit function

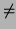Now suppose that f (a, b) = 0 and c = ($\partial$f /$\partial$y)(a, b) $\neq$ 0. We want to find the implicit function h(x) defined by f = 0 (see 7). We do this by showing that for each x near a there is a unique y so that f (x, y) = 0. Equivalently, we need to show that the function g(x, y) = y - f (x, y)/c has a unique fixed point for any chosen x near a.

Contractions give rise to functions with a unique fixed point.

Exercise 49   Let 0 < c < 1 be a constant. Let g(x) be a function so that g send the interval [a, b] to itself and | g(x) - g(y)| < c| x - y| for all x and y in [a, b]. Show that g(x₀) = x₀ for exactly one point x₀ in [a, b].

Consider the function g(x, y) = y - f (x, y)/c as above; we have g(a, b) = b and ($\partial$g/$\partial$y) = 0. For each fixed x we would like g(x, y) to be a contraction on some interval around b. As a first step:

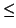
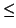
Exercise 50   Using the continuity of f₁ show that there is an interval [a - r, a + r] around a and an interval [b - s, b + s] around b so that |($\partial$g/$\partial$y)(x, y)| $\leq$ 1/2 for x and y in these respective intervals. (Hint: Write $\partial$g/$\partial$y in terms of f₁ to show that it is continuous). In particular, by the mean value theorem show that | g(x, y) - g(x, y')| $\leq$ 1/2(y - y') on these intervals.

Now by the continuity of f (and thus of g) we can choose a smaller r so that | g(x, b) - g(a, b)| 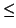$\leq$ s/2 for x in the interval [a - r, a + r]. Since g(a, b) = b, it follows that g(x, y) = b + (g(x, y) - g(x, b)) + (g(x, b) - g(a, b)) lies in the interval [b - s, b + s]. Applying the above exercise it follows that for every x there is a unique point y so that g(x, y) = y or equivalently f (x, y) = 0. We denote this point y as h(x). This function h is the required implicit function.

We have the identity,

$$\begin{multline*} h(x)-h(x')=g(x,h(x))-g(x',h(x'))= \\ \left(g(x,h(x))-g(x',h(x))\right) + \left(g(x',h(x))-g(x',h(x'))\right) \end{multline*}$$

Applying the mean value theorem to g(x', y) we obtain

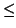
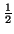
| h(x) - h(x')| $$\leq$$ | g(x, h(x)) - g(x', h(x)| + $${\textstyle\frac{1}{2}}$$| h(x) - h(x')|

Exercise 51   Use the above inequality and the continuity of g(x, y₀) for every fixed y₀ to conclude the h(x) is continuous.

Now if we assume in addition that f is differentiable to order k then it follows that h is also differentiable to order k by an entirely similar reasoning to the one in the above exercise.

Exercise 52   If f (x, y) has the form (near the point (a, b))

$$\begin{multline*} f(x,y) = f_{1,0}(x-a) + f_{0,1}(y-b) + \\ f_{2,0}(x-a)^2 + 2 f_{1,1}(x-a)(y-b) + f_{0,2}(y-b)^2 + o((x-a,y-b)^2) \end{multline*}$$

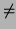
with f_{0, 1} $\neq$ 0, then show that the implicit function g(x) has the form (near x = a),

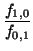
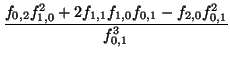
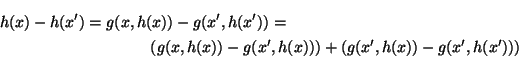
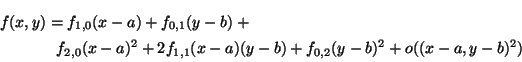
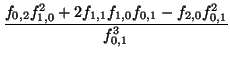g(x) = b - $${\frac{f_{1,0}}{f_{0,1}}}$$(x - a) + $${\frac{f_{0,2}f_{1,0}^2 + 2 f_{1,1}f_{1,0}f_{0,1} - f_{2,0}f_{0,1}^2}{f_{0,1}^3}}$$(x - a)² + o((x - a)²)