


Next: Curves
Up: New Functions from old
Previous: Implicit functions
We develop the theory of integration of continuous functions and prove
the fundamental theorem of calculus.
Let R be any (bounded) region in the plane which we want to measure
the area of. We can tile the plane with squares of unit length and
count the number of such squares that are contained in the region to
obtain an approximation to the area from below. On the other hand we
can count the number of squares that meet to region to obtain an
approximation to the area from above. We can repeat this with squares
of smaller size and appropriately scale the count it seems clear that
the approximant from below will increase and the approximant from
above will decrease. The least upper bound of the former is called the
inner measure and the greatest lower bound of the latter the outer
measure. To obtain an area for the region we must show that these two
numbers are the same; moreover, we would like these numbers to be
independent of the placement of the grid as well as rotation and/or
shearing of the grid.
Exercise 53
Show that the measure of any rectangle is the product of the two
sides. More generally, show that the area of a parallelogram is the
product of the height and the base.
Let f (x) be a (non-negative) continuous function for
a 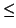 x
x 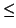 b. Let R be the region bounded by the lines x = a and x = b on the
left and right, by the x-axis below and the curve y = f (x) at the
top. By the previous exercise we can calculate the measure by using
rectangles instead of squares. We do this in the following exercise.
b. Let R be the region bounded by the lines x = a and x = b on the
left and right, by the x-axis below and the curve y = f (x) at the
top. By the previous exercise we can calculate the measure by using
rectangles instead of squares. We do this in the following exercise.
Exercise 54
By a partition
P of the interval [
a,
b] we mean a (finite)
collection of points
a =
t0 <
t1 <
... <
tn =
b. For any such
partition we define
mi (respectively
Mi) to be the minimum
(respectively maximum) value of
f (
x) for
ti - 1 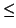 x
x 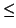 ti
ti.
- Show that the sum L(P, f ) (respectively U(P, f ))
approximate the area of the region from below (respectively
above), i. e. are sums of areas of rectangles enclosed by
(respectively enclosing) the region R.
| L(P, f ) |
= |
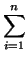 mi(ti - ti - 1) mi(ti - ti - 1) |
|
| U(P, f ) |
= |
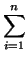 Mi(ti - ti - 1) Mi(ti - ti - 1) |
|
- If P' is a finer partition than P (i. e. each point of
P is also a point of P') then show that
L(
P,
f )
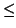 L
L(
P',
f )
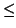 U
U(
P',
f )
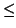 U
U(
P,
f )
- Let Pn denote the partition of [a, b] into n equal
parts. Show that
sup{
L(
P,
f )|
P a partition }
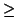
sup{
L(
Pn,
f )}
inf{
U(
P,
f )|
P a partition }
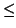
inf{
U(
Pn,
f )}
- Let i = i(P, f ) be such that the difference Mi - mi is
maximum. Then show that
U(
P,
f )-
L(
P,
f )
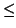
(
Mi -
mi)(
b -
a)
Let x(P, f ) denote the mid point of the interval
[ii - 1, ti] for this i.
- Let c be any point of the interval [a, b]. For any
positive
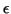 , show that there is a
, show that there is a 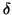 > 0 so that the
difference between the maximum and minimum values of f (x) on
the interval
[c -
> 0 so that the
difference between the maximum and minimum values of f (x) on
the interval
[c - 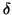 , c +
, c + 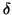 ] is less than
] is less than
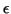 /(b - a). (Hint: use continuity of f at c).
/(b - a). (Hint: use continuity of f at c).
- The sequence
{xn = x(Pn, f )} has a convergent
subsequence
{yk = xnk}, with limit point c. Show that
there is a k0 so that if k
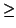 k0 and
i = i(Pnk, f )
then the entire sub-interval
[ti - 1, ti] of the partition
Pnk is contained in
[c -
k0 and
i = i(Pnk, f )
then the entire sub-interval
[ti - 1, ti] of the partition
Pnk is contained in
[c - 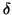 , c +
, c + 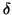 ].
].
- Deduce that
sup{L(Pnk, f )} = inf{U(Pnk, f )}.
- Conclude that the inner and outer measure of the region R
coincide.
This show that the area of the region R is well-defined. It is
denoted by
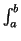 f to denote its depends on a, b and f (we
will justify the use of the
f to denote its depends on a, b and f (we
will justify the use of the 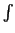 symbol below. First of all note
that
symbol below. First of all note
that
Exercise 55
Let
a <
c <
b and
f (
x) and
g(
x) be (positive) functions that are
continuous in the interval [
a,
b]; let
d > 0 be any positive
constant. Then we have
and
Due to this we are justified in extending the definition as
follows. If f (x) is continuous in the interval [a, b] and c > d
are points in this interval we define
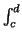 f : = -
f : = - 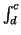 f. Moreover, if f is not everywhere positive we define
f. Moreover, if f is not everywhere positive we define
f+(x) = max{f (x,), 0} = (f (x) + | f (x)|)/2
and
f-(x) = max{ - f (x,), 0} = (- f (x) + | f (x)|)/2
Then clearly f± are positive functions and
f = f+ - f-. We
then define the integral of f by the formula
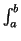 f : =
f : = 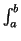 f+ -
f+ - 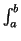 f-. This definition too is justified by the
additive property given above.
f-. This definition too is justified by the
additive property given above.
Now if f is continuous on an interval [a, b] where its minimum
value is m and its maximum value is M it is clear that
Exercise 56
Let
g(
x) =
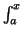 f
f, then
g is a differentiable function for all
points
x so that
a <
x <
b and its derivative is
f. (Hint: Apply
the addition rule and use continuity of
f at
x)
This justifies the use of the 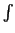 symbol. We have shown how to
analytically compute the function which we formally defined above.
In addition we have a way of constructing a function which is
differentiable and its derivative is continuous--a problem that was
raised in the section on continuous and differentiable functions.
symbol. We have shown how to
analytically compute the function which we formally defined above.
In addition we have a way of constructing a function which is
differentiable and its derivative is continuous--a problem that was
raised in the section on continuous and differentiable functions.



Next: Curves
Up: New Functions from old
Previous: Implicit functions
Kapil H. Paranjape
2001-01-20
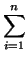 mi(ti - ti - 1)
mi(ti - ti - 1)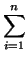 Mi(ti - ti - 1)
Mi(ti - ti - 1)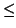 L(P', f )
L(P', f ) 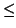 U(P', f )
U(P', f ) 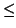 U(P, f )
U(P, f )
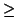 sup{L(Pn, f )}
inf{U(P, f )| P a partition }
sup{L(Pn, f )}
inf{U(P, f )| P a partition }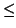 inf{U(Pn, f )}
inf{U(Pn, f )}
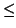 (Mi - mi)(b - a)
(Mi - mi)(b - a)
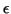 , show that there is a
, show that there is a 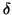 > 0 so that the
difference between the maximum and minimum values of f (x) on
the interval
[c -
> 0 so that the
difference between the maximum and minimum values of f (x) on
the interval
[c - 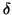 , c +
, c + 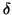 ] is less than
] is less than
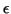 /(b - a). (Hint: use continuity of f at c).
/(b - a). (Hint: use continuity of f at c).
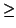 k0 and
i = i(Pnk, f )
then the entire sub-interval
[ti - 1, ti] of the partition
Pnk is contained in
[c -
k0 and
i = i(Pnk, f )
then the entire sub-interval
[ti - 1, ti] of the partition
Pnk is contained in
[c - 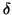 , c +
, c + 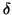 ].
].