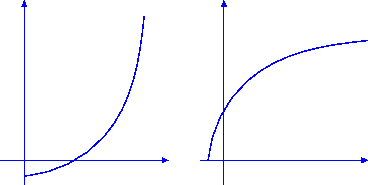
Exercise 47
If
f is continuously differentiable and
f'(
x0)
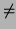
0 then show
that
f is monotonic in some interval around
x0. Hence show that
f has a inverse
g (as in the exercise above) in some small enough
interval around
f (
x0).
Exercise 48
If
f can be expressed as
f (x) = f (x0) + f1(x - x0) + ... + fn(x - x0)n + o((x - x0)n)
with
f1 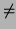
0, then show that the inverse function
g(
y) has the
following form where
y0 =
f (
x0).
g(
y) =
x0 +
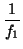
(
y -
y0) -
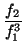
(
y -
y0)
2 + ... +
gn(
y -
y0)
n +
o((
y -
y0)
n)
where
gn is of the form
Pn(
f1,...,
fn)/
f1n + 1, where
Pn is a polynomial function.