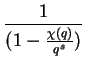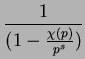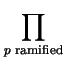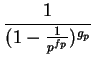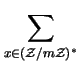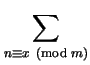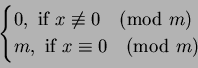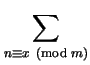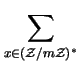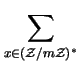Next: 4 Divisiblity of the
Up: Kummer's proof of Fermat's
Previous: Case 2: p| XYZ
We first need to introduce the Dedekind zeta function for a
number field K, and its Euler product expansion
where the sum runs over all ideals I of R and the product runs
over all prime ideals Q of R. The two expressions give us two ways
of computing
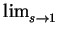 (s - 1)
(s - 1)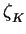 (s). The left-hand side is
expressed in terms of ``arithmetic'' invariants and the right-hand
side in terms of invariants for the Galois group. The resulting
identity gives a way for computing the Class number h of K.
The left-hand limit can be computed to be
The set
{I | N(I)
(s). The left-hand side is
expressed in terms of ``arithmetic'' invariants and the right-hand
side in terms of invariants for the Galois group. The resulting
identity gives a way for computing the Class number h of K.
The left-hand limit can be computed to be
The set
{I | N(I) 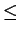 r} can be split according to ideal
classes. We try to compute for each ideal class C,
r} can be split according to ideal
classes. We try to compute for each ideal class C,
z(
C) =
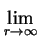
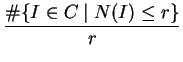
.
Fixing an ideal I0 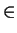 C, this latter
set is bijective to the set
{aR
C, this latter
set is bijective to the set
{aR 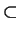 I0-1 | N(a)
I0-1 | N(a) 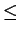 r . N(I0)-1}.
(Here N(a) denotes the modulus of the norm of a.)
We have a natural embedding
K
r . N(I0)-1}.
(Here N(a) denotes the modulus of the norm of a.)
We have a natural embedding
K 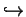 K
K 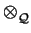
 R. The image
of
J = I0-1 is a lattice in
K
R. The image
of
J = I0-1 is a lattice in
K 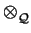
 R. Let
R. Let 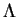 denote the image of J - {0} in the quotient
denote the image of J - {0} in the quotient
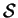 = (K
= (K 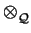
 R)*/U where U is the image of the group
of units in R under the above embedding. There is a natural
homomorphism
N :
R)*/U where U is the image of the group
of units in R under the above embedding. There is a natural
homomorphism
N : 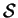
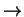
 R* which restricts to the modulus of the
norm on the image of K. We obtain a natural bijection between
{aR
R* which restricts to the modulus of the
norm on the image of K. We obtain a natural bijection between
{aR 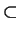 I0-1 | N(a)
I0-1 | N(a) 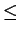 r}
and
{l
r}
and
{l 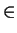
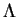 | N(l )
| N(l ) 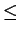 r}. Let
r}. Let 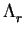 denote the
image of
(1/r)J - {0} in
denote the
image of
(1/r)J - {0} in 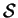 , then we have a natural bijection
between
{l
, then we have a natural bijection
between
{l 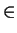
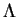 | N(l )
| N(l ) 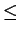 rd}
and
{l
rd}
and
{l 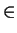
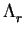 | N(l )
| N(l ) 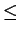 1},
where d denotes the degree of K oover
1},
where d denotes the degree of K oover  Q.
Let
Q.
Let
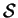
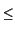 1 denote locus of
l
1 denote locus of
l 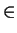
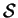 such that
N(l )
such that
N(l ) 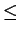 1. Let
1. Let 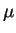 denote the Haar measure
on
K
denote the Haar measure
on
K 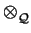
 R. This is invariant under the action of U
and thus gives a measure also denoted by
R. This is invariant under the action of U
and thus gives a measure also denoted by 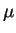 on
on 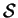 . Since J is
a lattice in
K
. Since J is
a lattice in
K 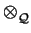
 R we have
Moreover, the denominator can be re-written
In particular, we see that the limit z(C) is independent of the
class C. Let
(K
R we have
Moreover, the denominator can be re-written
In particular, we see that the limit z(C) is independent of the
class C. Let
(K 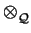
 R)*1 denote the kernel of the
norm map. This is a group and thus we have a Haar measure
R)*1 denote the kernel of the
norm map. This is a group and thus we have a Haar measure 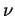 on
it. One shows that
Combining the above calculations one obtains
This often called the ``Class number formula'' for K. Note that the
denominator can be computed in closed form in terms of the
discriminant D of the field K and the number of pairs of
conjugate complex embeddings r2 of K.
However, the numerator is in general
more complicated since it involves computing the group of units of
K.
To expand the right-hand term we restrict our attention to abelian
extensions K of
on
it. One shows that
Combining the above calculations one obtains
This often called the ``Class number formula'' for K. Note that the
denominator can be computed in closed form in terms of the
discriminant D of the field K and the number of pairs of
conjugate complex embeddings r2 of K.
However, the numerator is in general
more complicated since it involves computing the group of units of
K.
To expand the right-hand term we restrict our attention to abelian
extensions K of  Q. The product term on the left can be first
grouped according to rational primes
Now for each rational prime q which is unramified in K we have
where
Q. The product term on the left can be first
grouped according to rational primes
Now for each rational prime q which is unramified in K we have
where 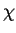 runs over all characters of the Galois group and
runs over all characters of the Galois group and
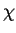 (q) =
(q) = 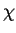 (Frobq) is the value of
(Frobq) is the value of 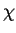 on a Frobenius element
associated with q. We define the Dirichlet L-series and their
Euler product formulas as follows
where we set
on a Frobenius element
associated with q. We define the Dirichlet L-series and their
Euler product formulas as follows
where we set 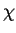 (p) = 0 when
(p) = 0 when 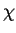 is ramified at p. We also
define the additional factor
is ramified at p. We also
define the additional factor
F(
s) =
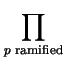
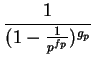
where the product runs over all ramified primes and fp denotes the
residue field extension over p and gp the number of distinct
primes in K lying over p. The product expansion of
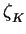 (s)
becomes
Thus the computation of the limit can be reduced to the corresponding
computation for the Dirichlet L-series. For the case of the unit
character we get by comparison with the zeta function
(s)
becomes
Thus the computation of the limit can be reduced to the corresponding
computation for the Dirichlet L-series. For the case of the unit
character we get by comparison with the zeta function
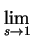
(
s - 1)
F(
s)
L(
s, 1) = 1.
So the right-hand limit gives
There is a positive integer m such that 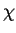 is determined
on classes modulo m and
is determined
on classes modulo m and 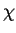 is zero on all primes p dividing
it; m is called the conductor of
is zero on all primes p dividing
it; m is called the conductor of 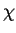 . We rewrite the
L-function associated with
. We rewrite the
L-function associated with 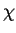 as follows
The latter sum can be rewritten using the identity
where
as follows
The latter sum can be rewritten using the identity
where 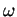 is a primitive m-th root of unity. The second sum
then becomes
Thus we obtain
The expression
is called the Gaussian sum associated with the integer i and the
character
is a primitive m-th root of unity. The second sum
then becomes
Thus we obtain
The expression
is called the Gaussian sum associated with the integer i and the
character 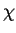 . If
. If 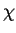 is not the unit character then
is not the unit character then
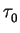 (
(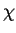 ) = 0. Moreover, if i
) = 0. Moreover, if i 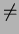 0 then we have the identity
Hence, we obtain the formula when
0 then we have the identity
Hence, we obtain the formula when 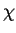 is not the unit character
is not the unit character



Next: 4 Divisiblity of the
Up: Kummer's proof of Fermat's
Previous: Case 2: p| XYZ
Kapil Hari Paranjape
2002-11-22
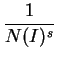 =
= 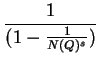
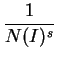 =
= 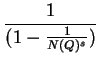
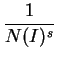 =
= 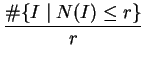
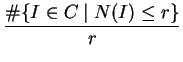 .
.
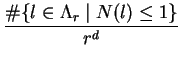 =
= 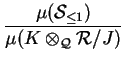
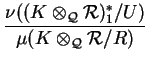
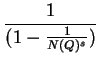 =
= 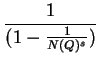
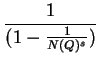 =
=