


Next: 3 Transcendental computation of
Up: 2 Construction of cyclic
Previous: Case 1: p |
We may assume that Z = pkZ0 and
(p, X, Y, Z0) are mutually
co-prime. By writing
p = (unit) . 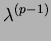 in the ring
R, we obtain an equation of the form
in the ring
R, we obtain an equation of the form
Up +
Vp + (unit)
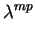 Wp
Wp = 0 with
m > 0
where (U, V, W) are in R so that
(U, V, W,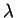 ) are mutually
co-prime. Let (U, V, W) be a collection of elements of R that
satisfy such an equation with m the least possible. Then
) are mutually
co-prime. Let (U, V, W) be a collection of elements of R that
satisfy such an equation with m the least possible. Then 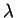 divides one of the factors
(U +
divides one of the factors
(U + 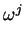 V). But then we have
V). But then we have
(
U +
 V
V) - (
U +
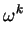 V
V) =

(1 -

)
V = (unit)
. 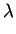 V
V
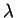 divides all the factors
(U +
divides all the factors
(U + 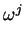 V).
Moreover, since V is co-prime to p and thus
V).
Moreover, since V is co-prime to p and thus 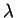 as well, we
see that
(U +
as well, we
see that
(U + 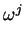 V)/
V)/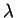 have distinct residue classes modulo
have distinct residue classes modulo
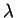 R. But then, by the pigeon-hole principle there is at least
one
0
R. But then, by the pigeon-hole principle there is at least
one
0 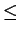 j
j 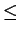 (p - 1) such that
(U +
(p - 1) such that
(U + 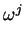 V) is divisible by
V) is divisible by
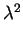 in R. Replacing V by
in R. Replacing V by
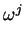 V we may assume that
(U + V) is divisible by
V we may assume that
(U + V) is divisible by 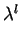 for some l > 1. Hence we may write
for some l > 1. Hence we may write
| U + V |
= |
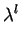 a0 a0 |
|
U + 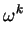 V V |
= |
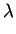 ak; fork > 0 ak; fork > 0 |
|
where all the ak are elements of R that are co-prime to
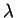 and with each other (as in the previous case). This gives us
the identity
l + (p - 1) = mp or equivalently
l = (m - 1)p + 1. Since
l
and with each other (as in the previous case). This gives us
the identity
l + (p - 1) = mp or equivalently
l = (m - 1)p + 1. Since
l 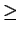 2 we have m
2 we have m 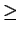 2.
Now by unique factorisation of ideals in R we see that there
are ideals Ij in R such that
Ijp = ajR. Assume that I0,
I1 and Ip - 1 are principal, then we have the equations
2.
Now by unique factorisation of ideals in R we see that there
are ideals Ij in R such that
Ijp = ajR. Assume that I0,
I1 and Ip - 1 are principal, then we have the equations
| U + V |
= |
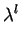 . u . b0p . u . b0p |
|
U + 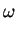 V V |
= |
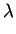 . v . b1p . v . b1p |
|
U + 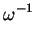 V V |
= |
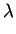 . w . b-1p . w . b-1p |
|
for some units u, v and w in R and some elements b0,
b1 and b-1 in R. Eliminating U and V from these
equations we obtain
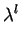 . u . b0p
. u . b0p -
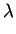 . v . b1p
. v . b1p =
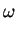
(
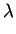 . w . b-1p
. w . b-1p -
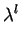 . u . b0p
. u . b0p)
which becomes
b1p +
v1 . b-1p +
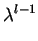 . v2b0p
. v2b0p = 0
where v1 and v2 are units (we use here the fact that 1 + 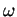 is a unit in R). Modulo pR the last term on the left-hand side
vanishes since
l
is a unit in R). Modulo pR the last term on the left-hand side
vanishes since
l 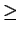 p > (p - 1). Thus we see that v1 is congruent
to a p-th power and thus an integer modulo pR. By section 1 we
have a representation of Galois as required, unless v1 is a p-th
power. If v1 = v3p, then
(U, V, W) = (b1, v3b-1, b0) satisfy
p > (p - 1). Thus we see that v1 is congruent
to a p-th power and thus an integer modulo pR. By section 1 we
have a representation of Galois as required, unless v1 is a p-th
power. If v1 = v3p, then
(U, V, W) = (b1, v3b-1, b0) satisfy
Up +
Vp + (unit)
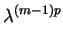 Wp
Wp = 0
which contradicts the minimality of m since we have seen that
m 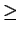 2. Thus, either we have constructed a cyclic extension of the
required type or one of I0, I1, Ip - 1 is non-principal. But
then again by the principal result of Class Field theory we have a
cyclic extension as required.
2. Thus, either we have constructed a cyclic extension of the
required type or one of I0, I1, Ip - 1 is non-principal. But
then again by the principal result of Class Field theory we have a
cyclic extension as required.



Next: 3 Transcendental computation of
Up: 2 Construction of cyclic
Previous: Case 1: p |
Kapil Hari Paranjape
2002-11-22