


Next: Bibliography
Up: Kummer's proof of Fermat's
Previous: 3 Transcendental computation of
Combining the results of sections 1 and 2 we have shown that
any counter-example to Fermat's Last theorem for a prime p 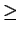 5
leads to a non-trivial representation
which is unramified everywhere; here K denotes the subfield of
complex numbers generated by the p-th roots of unity. Kummer called
primes which admit such representations irregular. He showed
that there are indeed such primes (p = 37 is one such) and hence this
particular attempt to prove Fermat's Last theorem fails. We now wish
to show how one goes about checking whether a prime is
irregular.
We apply the results of Section 3 in the special case where
K is the prime cyclotomic field of section 1 and also to the
totally real subfield L.
First of all we use the divisibility of the class number h of R
by the class number h+ of S to write
h = h+ . h- for
some integer h-. Let W denote the (finite cyclic) group of
roots of unity in K. Then we have
U = W . U+, where U+
denotes the group of units in S and so
#(U/U+) = #(W/{±1}) = p. We have the natural inclusion
L
5
leads to a non-trivial representation
which is unramified everywhere; here K denotes the subfield of
complex numbers generated by the p-th roots of unity. Kummer called
primes which admit such representations irregular. He showed
that there are indeed such primes (p = 37 is one such) and hence this
particular attempt to prove Fermat's Last theorem fails. We now wish
to show how one goes about checking whether a prime is
irregular.
We apply the results of Section 3 in the special case where
K is the prime cyclotomic field of section 1 and also to the
totally real subfield L.
First of all we use the divisibility of the class number h of R
by the class number h+ of S to write
h = h+ . h- for
some integer h-. Let W denote the (finite cyclic) group of
roots of unity in K. Then we have
U = W . U+, where U+
denotes the group of units in S and so
#(U/U+) = #(W/{±1}) = p. We have the natural inclusion
L 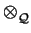
 R
R 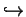 K
K 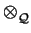
 R from which we obtain
the isomorphism
R from which we obtain
the isomorphism
(
K 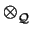
 R
R)
*1/(
L 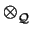
 R
R)
*1 = (
 C*1
C*1/
 R*1
R*1)
(p - 1)/2
 Q. From this we deduce
that
Q. From this we deduce
that
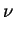
((
K 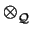
 R
R)
*1/
U) =
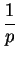 .
. 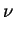
(
 C*1
C*1/
 R*1
R*1)
(p - 1)/2 . 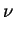
((
L 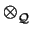
 R
R)
*1/
U+)
The formula for computing discriminants yields
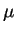
(
K 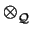
 R
R/
R) =
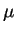
(
L 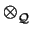
 R
R/
S)
2 . p1/2
since p is the norm of the relative discrimant. Thus the class
number formulas for K and L then give a formula for h-
Hence h- can be computed explicitly and in closed form. In
particular, the divisibility of h- by p is an easily computable
criterion.
The divisibility of h+ by p is more complicated. As remarked
earlier, the term
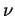 ((L
((L 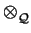
 R)*1/U+) is
difficult to compute. However, we have the subgroup
U+ , cycl = U+
R)*1/U+) is
difficult to compute. However, we have the subgroup
U+ , cycl = U+ 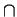 Ucycl and one can compute
Ucycl and one can compute
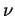 ((L
((L 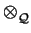
 R)*1/U+ , cycl). In fact one
shows that
R)*1/U+ , cycl). In fact one
shows that
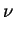
((
L 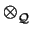
 R
R)
*1/
U+ , cycl) =
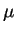
(
L 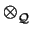
 R
R/
S)
. 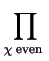 L
L(1,
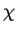
)
where the product runs over all non-trivial characters 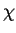 such
that
such
that
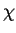 (- 1) = 1. The class number formula for h+ becomes
(- 1) = 1. The class number formula for h+ becomes
h+ = [U+ : U+ , cycl] = [U : Ucycl].
This is the first coincidence that makes Kummer's calculations
possible.
From the above identity we see that if p divides h+ then we
have a real unit u such that its p-th power is a cyclotomic unit
but u is not itself cyclotomic. Hence v = up is a cyclotomic unit
which is congruent to an integer modulo pS. If we find a
w 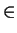 Ucycl such that v = wp then one shows easily that u is
itself a cyclotomic unit. Let Q denote the quotient group
(S/pS)*/(
Ucycl such that v = wp then one shows easily that u is
itself a cyclotomic unit. Let Q denote the quotient group
(S/pS)*/( Z/p
Z/p Z)*. We obtain a natural homomorphism
which is represented by a square matrix with entries from
Z)*. We obtain a natural homomorphism
which is represented by a square matrix with entries from
 Fp.
The preceding remarks imply that p| h+ only if det(m) = 0. The
second coincidence that makes Kummer's calculation work is
that
det(m)
Fp.
The preceding remarks imply that p| h+ only if det(m) = 0. The
second coincidence that makes Kummer's calculation work is
that
det(m) 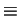 h-(mod p).
Thus we see that p| h if and only if p| h-. Hence we can easily
check which primes are regular.
to3em
h-(mod p).
Thus we see that p| h if and only if p| h-. Hence we can easily
check which primes are regular.
to3em



Next: Bibliography
Up: Kummer's proof of Fermat's
Previous: 3 Transcendental computation of
Kapil Hari Paranjape
2002-11-22
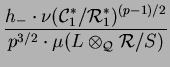 =
= 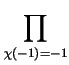 L(1,
L(1,