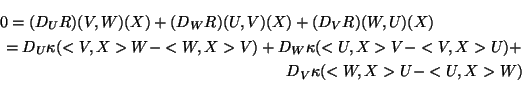4 Manifolds all of whose geodesics are lines

In order to tie up the first two sections we need to have a notion analogous to lines in a general Riemannian manifold--this is provided by geodesics or energy minimising paths.

Figure 10: A Geodesic

To a stationary observer placed on the manifold it would appear that a body travelling along an energy minimising path is subject to no acceleration. The translation of this into differential geometric terms is D_X(t)(X(t)) = 0 where X(t) is the tangent vector at time t. By the theory of second order ordinary differential equations there is a unique geodesic starting at a point p with initial velocity $\;\stackrel{\rightarrow}{v}\;$ for any choice of p and $\;\stackrel{\rightarrow}{v}\;$.

A result of Whitehead shows that for any point p there is a small region M surrounding it so that there is a unique geodesic in M joining any pair of points in M. The notion of between-ness is defined by saying that B lies between A and C in M if B lies on the (unique) geodesic joining A and C. Extending the geodesic within M beyond B and before A gives us the ``line'' joining A and B. We then easily check that Veblen's axioms of local geometry other than those involving planes are satisfied. In particular we have trouble verifying the Pasch axiom--numbered 7 in the list of Veblen's axioms given in section 1.

Let us therefore make the additional assumption that these axioms dealing with planes are satisfied; we will show that this imposes a restriction on the curvature of the Riemannian manifold M, which is satisfied if and only if M is a convex region in one of the ``classical'' geometries--Euclidean, Hyperbolic or Projective.

According to the results of section 1 we can choose coordinates on M in such a way that the geodesics are mapped into lines. In terms of these coordinates we see that a geodesic must be an accelerated path:

$$\nabla_{X(t)}^{}$$(X(t)) = D_X(t)(X(t)) - $$\omega$$(X(t))(X(t)) = - $$\omega$$(X(t))(X(t))

being the acceleration at time t. Since the geodesics are lines it follows that acceleration is proportional to X(t); since this is to happen for geodesics in all directions

$$\omega$$($$\;\stackrel{\rightarrow}{v}\;$$)($$\;\stackrel{\rightarrow}{v}\;$$) = $$\lambda_{\vec{v}}^{}$$ ^. $$\;\stackrel{\rightarrow}{v}\;$$

for some scalar $\lambda_{\vec{v}}^{}$ depending on $\;\stackrel{\rightarrow}{v}\;$. In addition we have the torsion-free condition and the linearity of $\omega$ in each variable. It follows that $\lambda_{X}^{}$ = < $\Lambda$, X > is a linear functional associated with some vector field $\Lambda$

$$\omega$$($$\;\stackrel{\rightarrow}{v}\;$$)($$\;\stackrel{\rightarrow}{w}\;$$) = $${\textstyle\frac{1}{2}}$$( < $$\Lambda$$(p),$$\;\stackrel{\rightarrow}{v}\;$$ > ^. $$\;\stackrel{\rightarrow}{w}\;$$ + < $$\Lambda$$(p),$$\;\stackrel{\rightarrow}{w}\;$$ > ^. $$\;\stackrel{\rightarrow}{v}\;$$)

Thus we have

$$\begin{multline*} R(X,Y)Z = D_X(D_Y(Z)) - D_Y(D_X(Z)) -D_{L_X (Y)}(Z) \\ = \f... ...t X \\ - <\Lambda,Z>(<\Lambda,X>\cdot Y - <\Lambda,Y>\cdot X)) \end{multline*}$$

Let X and Y be orthogonal then

K(X, Y, X, Y) = < R(X, Y)X, Y > = < D_X($$\Lambda$$), X > < Y, Y > - < $$\Lambda$$, X > ² < Y, Y >

Thus the sectional curvature becomes

$$\kappa$$(X, Y) = $${\frac{<\Lambda,X>^2 - <D_X(\Lambda),X>}{<X,X>^2}}$$

where the right hand side does not depend on Y! Thus by symmetry it does not depend on X either.

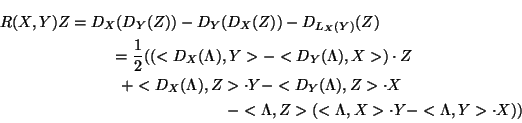
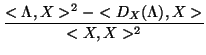
Now we have $\kappa$(X, Y)(p) = $\kappa$(p) depends only on the point p. Thus we have

K(X, Y, Z, W) = $$\kappa$$ ^. ( < X, W > < Y, Z > - < X, Z > < Y, W > )

and hence

R(X, Y)(Z) = $$\kappa$$ ^. ( < Y, Z > X - < X, Z > Y)

Now applying the second identity proved by Bianchi

$$\begin{multline*} 0= (D_U R)(V,W)(X) + (D_W R)(U,V)(X) + (D_V R)(W,U)(X)\\ = ... ... D_W\kappa (<U,X>V - <V,X>U) + \\ D_V\kappa (<W,X>U - <U,X>W) \end{multline*}$$

So that if U = X is orthogonal to V and W we get

0 = D_W$$\kappa$$ ^. < U, U > V - D_V$$\kappa$$ ^. < U, U > W

Finally, since have assumed that we are in (at least) three dimensions we can assume that V and W are linearly independent and < U, U > $\neq$ 0, so that we obtain D_W$\kappa$ = 0. Since W is arbitrary this just means that $\kappa$ is the constant function. Now, by applying the result of Cartan and Hadamard mentioned in the previous section we see that our local Riemannian space M has to be contained in one of the ``classical'' geometries--Euclidean, Hyperbolic or Projective.