


Next: Manifolds
Up: Coordinate Geometry
Previous: Curves
As in the case of curves we will begin with the study of a surface S
defined by a single equation
f (x, y, z) = 0 and eventually treat more
general surfaces. If
p = (x0, y0, z0) is a point on S, and a line
l through p is given in parametric form
(x0 + tx1, y0 + ty1, z0 + tz1), then we can define the order of
contact r(l, S, p) as the highest power of t which divides the the
function
F(t) = f (x0 + tx1, y0 + ty1, z0 + tz1). A tangent line is then
one which has the largest order of contact among all lines. The locus
of all tangent lines describes a conical surface with vertex p. In
fact,
Exercise 10
Either
r(
l,
S,
p)
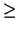
2 for all lines through
p or
there is a plane
P so that lines
l with
r(
l,
S,
p)
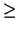
2 are
precisely lines lying in the plane and passing through
p. The latter
case occurs if and only if the vector
(
fx(
p),
fy(
p),
fz(
p)) is
non-zero. By a replacing the equation
f = 0 by a non-zero multiple we
can ensure that the vector (
fx(
p),
fy(
p),
fz(
p)) is a unit vector,
which is then called the
unit normal to the surface.
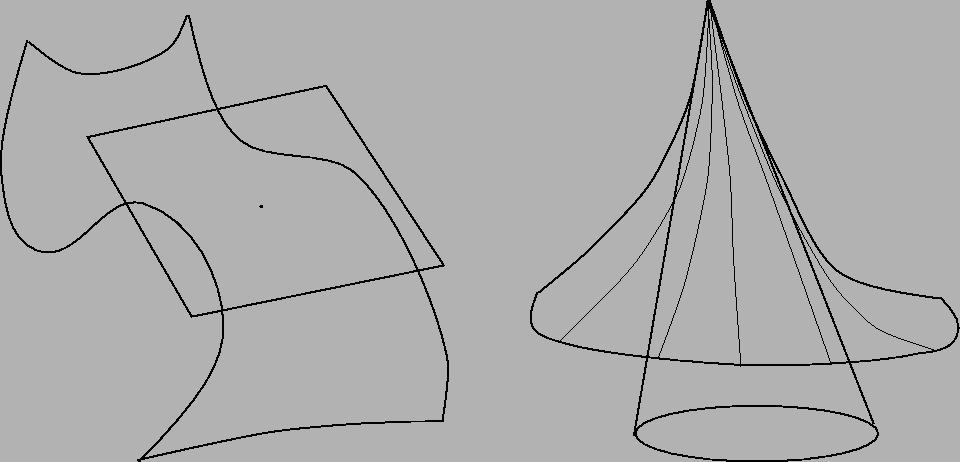
As in the case of curves we call the former case the singular
surfaces and the latter are called smooth or non-singular
surfaces. We will restrict our attention to smooth surfaces.
picture(9565,5259)(556,-4750)
(991,-4696)(0,0)[lb]Smooth surface and its plane of tangent lines
(6166,-4696)(0,0)[lb]Singular surface and its cone of tangents
We define the linear space of tangent vectors Tp(S) to S at p
as the space of all vectors v so that the parametric line p + tv is
tangent to S at p.
Exercise 11
Show that the tangent space is precisely,
{v = (x1, y1, z1) | fx(x0, y0, z0)x1 + fy(x0, y0, z0)y1 + fz(x0, y0, z0)z1}
In other words
v is tangent if and only if
Dv(
f )(
p) = 0.
The curvature of curves defined in the previous section can be
formulated as follows. We have a map from a plane curve C to the
unit circle given by sending each point to the unit tangent vector at
that point (we need to choose a ``direction'' along the curve but that
can be done locally). As we saw the derivative of this map is the
curvature. Now the unit normal direction is a right-angle rotation from
the tangent vector, so we could equally well have used the map which
takes a point to its unit normal. The latter map also makes sense for
a surface S in 3-space; we have a natural map
p 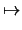 n
n(
p) =
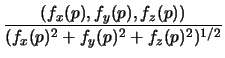
which sends S to the (unit) sphere. Curvature should be a measure of
the derivative of this map. Let v be any vector in Tp(S) or
equivalently v be a vector orthogonal to n(p).
Exercise 12
Show that Dv(n)(p) is orthogonal to n(p)
also. (Hint: Use the equation
n . n = 1 for all p).
Thus, if v and w are linearly independent vectors in Tp(S) (and
hence form a basis of this vector space), then we have
Dv(n)(p) = av + bw andDw(n)(p) = cv + bw
for some constants a, b, c and d.
Definition 4
We define the Gaussian curvature of S at p to be the
determinant ad - bc of the above linear transformation.
Exercise 13
Show that for any function f, vectors v, w and
constant a we have
D(av + w)(f )= aDv(f )+ Dw(f ). Now show that
the above definition is independent of the choice of vectors v and
w.
We can additionally justify the above definition by noting that the
Gaussian curvature of a plane is 0. In order to understand the
Gaussian curvature better we must first understand the notion of
``straight lines'' or geodesics. To begin with let us examine
curves lying on the surface. Let
p = (x0, y0, z0) be a point of S
and
(x(t), y(t), z(t)) be a curve on S passing through p at t = 0.
Exercise 14
Show that the tangent vector
(xt(0), yt(0), zt(0)) is
in the tangent space Tp(S).
We have already seen that a curve has non-trivial curvature if the
acceleration required to travel along it at constant speed is
non-zero. Thus a curve must be considered straight on the
surface S if the projection of this acceleration into
Tp(S) is zero. In other words:
Definition 5
Let
(
x(
t),
y(
t),
z(
t)) be a parametrised curve (of some
order
r 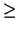
2) on the surface
S. Moreover, suppose that the
speed
((
xt)
2 + (
yt)
2 + (
zt)
2)
1/2 is a constant. We say that
the curve is
geodesic on
S if the acceleration at any point
of the curve is a multiple of the unit normal to
S at that point.
Exercise 15
Consider a parametric solution of order 3 to the
equations
f (
x(
t),
y(
t),
z(
t)) = 0 and
(
xt)
2 + (
yt)
2 + (
zt)
2 =
c;
morover suppose that the acceleration is a multiple of the normal to
S. Show that we obtain the equation for the acceleration vector
(
x2,
y2,
z2) = -
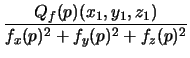
(
fx(
p),
fy(
p),
fz(
p))
where,
p = (
x0,
y0,
z0) is the ``starting point'',
(
x1,
y1,
z1) is
the initial tangent vector and
Qf is the quadratic form given by
the second derivatives of
f, that is
Qf(a, b, c) = fxxa2 + 2fxyab + 2fxzac + fyyb2 + 2fyzbc + fzzc2
The above equation can be written as
(
xtt,
ytt,
ztt)(
p) = -
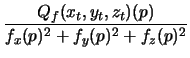
(
fx(
p),
fy(
p),
fz(
p))
Consider the quadratic form Q obtained by restricting the form
Qf/(fx2 + fy2 + fz2)1/2 to the tangent space Tp(S).
Theorem 1
Let
Q be a quadratic form on a vector space
V (over
the real numbers) there is an orthonormal basis
{
e1,...,
en} of
V so that
Q can be written as
Q(u1e1 + ... + unen) = a1u12 + ...anen2
In particular, we have an orthonormal basis
{e1, e2} for the
tangent space Tp(S) so that
Q(ue1 + ve2) = ku2 + lv2.
Euler called the numbers k and l the principal curvatures of S.
Exercise 16
Show that the Gaussian curvature of S is kl.
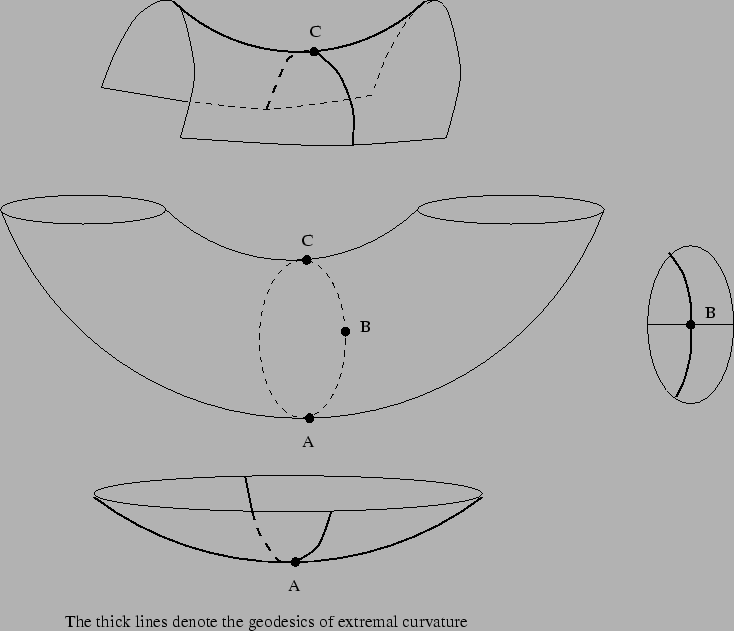
picture(7682,6596)(2092,-7465)
Examples of different curvatures on a tube
We shall now show how one can use geodesics to compute curvature. Let
p be any point on the surface S, then for each tangent direction
w in Tp(S) we can form the parametric geodesic
gp, w(t) of
some order r. Let e1, e2 be a basis of Tp(S) as above and
w = ue1 + ve2. Consider the map
(
u,
v)
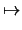 p
p(
u,
v) =
gp, ue1 + ve2(1)
To simplify things we take p to be the origin (by translation) and
let e3 to be the unit normal to S at p. We use
{e1, e2, e3} as a basis in which to express points of space. The
above map then becomes (for r = 4),
p(u, v) = (u + A(u, v), v + B(u, v), - frac12Q(u, v) + C(u, v))
where A, B and C are homogeneous of degree 3.
Exercise 17
By using the geodesic equation show that
A = Q(u, v)Qu(u, v)/6 and
B = Q(u, v)Qv(u, v)/6.
By definition of p(u, v) the lines through the origin in the (u, v)
plane go to geodesics in S. What about other lines? Consider the
line
l = (u0 + su1, v0 + sv1) parametrised by s in the (u, v) plane.
It becomes a curve
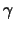 (s) = p(u0 + su1, v0 + sv1) in space. The
velocity vector of this curve is
(s) = p(u0 + su1, v0 + sv1) in space. The
velocity vector of this curve is
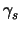 (s) = puu1 + pvv1 and
the acceleration is
(s) = puu1 + pvv1 and
the acceleration is
a(
s) =
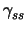
(
s) =
puuu12 + 2
puvu1v1 +
pvvv12
We need to find the component of this accleration in the tangent plane
to S, i. e. is the space of pu and pv.
Exercise 18
Prove the following formulas valid modulo order 2 in
u0
and
v0
| a(s) . pu |
= |
kl /3v1(v0u1 - u0v1) |
|
| a(s) . pv |
= |
kl /3u1(v0u1 - u0v1) |
|
One checks that pu and pv are unit vectors modulo order 2 in
u0 and v0. Thus, the magnitude of the acceleration is
(kl /3)(v0u1 - u0v1) times the length of the vector (u1, v1)
along the line l in the (u, v) plane. Thus the curvature of the
image of lines parallel to the origin in the (u, v) plane is also
related to the Gaussian curvature of S; which thus also measures the
deviation from the parallel postulate.



Next: Manifolds
Up: Coordinate Geometry
Previous: Curves
Kapil H. Paranjape
2001-01-20
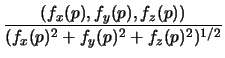
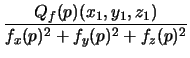 (fx(p), fy(p), fz(p))
(fx(p), fy(p), fz(p))
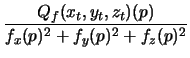 (fx(p), fy(p), fz(p))
(fx(p), fy(p), fz(p))
![]() (s) = p(u0 + su1, v0 + sv1) in space. The
velocity vector of this curve is
(s) = p(u0 + su1, v0 + sv1) in space. The
velocity vector of this curve is
![]() (s) = puu1 + pvv1 and
the acceleration is
(s) = puu1 + pvv1 and
the acceleration is