


Next: Suggested Reading
Up: Coordinate Geometry
Previous: Surfaces
We can try to generalise the above results from two variables u, v
to n variables u1, ..., un for any positive integer n. A
manifold M in parametric form is the locus of points (in some
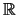 k) obtained as the image of a vector-valued function
x(u1,..., un). Moreover, to ensure that we have n ``directions
of freedom'' we also require the derivatives xu1, ...,
xun to be a linearly independent set at every point; we use
Tp(M) to denote the linear span of these vectors which is called
the tangent space to M at p. (For those who know more, this is a
local manifold and not a global one).
k) obtained as the image of a vector-valued function
x(u1,..., un). Moreover, to ensure that we have n ``directions
of freedom'' we also require the derivatives xu1, ...,
xun to be a linearly independent set at every point; we use
Tp(M) to denote the linear span of these vectors which is called
the tangent space to M at p. (For those who know more, this is a
local manifold and not a global one).
If
(u1(t),..., un(t)) is an n-tuple of functions of one
variable we obtain a curve in M. The velocity and acceleration of
this curve as a curve in
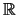 k are
k are
| v |
= |
xu1u1, t + ... + xunun, t and |
|
| a |
= |
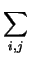 xuiujui, tuj, t xuiujui, tuj, t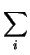 xuiui, tt xuiui, tt |
|
The vector v is in the tangent space to M. We need to understand
the projection of acceleration into the tangent space to see whether a
curve is indeed ``curved'' in M or is a geodesic.
Exercise 19
Let
v1, ...,
vn be linearly independent
vectors. Show that the matrix whose
ij-th entry is
gij =
vi . vj is a positive definite symmetric matrix. Let
hij denote the matrix entries of its inverse. The orthogonal
projection of a vector
a to the linear span of
v1, ...,
vn
is given by
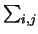 hij
hij(
a . vi)
vj.
Thus we see that the orthogonal projection of the acceleration into
the tangent space of M is given by
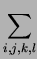
(
hkl(
xuiuj . xuk)
ui, tuj, t)
xul +
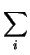 ui, ttxui
ui, ttxui
Where we will use
gij = (xui . xuj) and hij for the
matrix entries of the inverse of the matrix (gij). Now we have
the following equations for the derivatives of gij
(gij)uk = (xuiuk . xuj) + (xui . xujuk)
We ``solve'' these to obtain
(xuiuj . xuk) = (1/2)((gik)uj + (gjk)ui - (gij)uk)
Finally, we can put
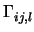
=
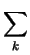 hkl
hkl(1/2)((
gik)
uj + (
gjk)
ui - (
gij)
uk)
so that the components of acceleration along xuk are given by
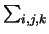
 ui, tuj, t + uk, tt.
ui, tuj, t + uk, tt.
First of all we note that the
 and hence the
acceleration of a curve on M can be computed one we are given the
gij as functions of ui. We no longer need the ``crutch'' of
the vector-valued functions x(ui). Thus, the geometry of the
manifold M is entirely described by the matrix-valued function
(gij) with values in positive-definite matrices. This function
gives the speed of a curve (ui(t)) as
and hence the
acceleration of a curve on M can be computed one we are given the
gij as functions of ui. We no longer need the ``crutch'' of
the vector-valued functions x(ui). Thus, the geometry of the
manifold M is entirely described by the matrix-valued function
(gij) with values in positive-definite matrices. This function
gives the speed of a curve (ui(t)) as
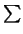 gijui, tuj, t and the accleration is given by the formula above.
gijui, tuj, t and the accleration is given by the formula above.
Exercise 20
Use the geodesic normal form of the surface as given
above and compute the speed of a curve
(
u(
t),
v(
t)) to be
ut2 + vt2 + (kl /3)(uvt - vut)2
modulo order 3 terms in
u and
v.
Thus the curvature can also be obtained by comparing the speed of
curves with the ``usual'' speed in the (u, v) plane. We shall see
that this is the key idea used by Riemann to understand curvature in
many dimensions.
Secondly, we note that the equation for a curve on M with 0
accleration can easily be solved inductively given the starting
point and the velocity at that point. In other words given
(u1, 0,..., un, 0) and
(u1, 1,..., un, 1) we consider a
curve given by the functions
ui(t) = ui, 0 + ui, 1t + .... By comparing the coefficients of tr in the equation
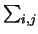
 ui, tuj, t + uk, tt = 0, we can
inductively solve for ui, 2, ui, 3 and so on.
ui, tuj, t + uk, tt = 0, we can
inductively solve for ui, 2, ui, 3 and so on.
Let p be a fixed point on M and choose a collection of vectors
e1, ...en so that (gij) becomes the identity matrix with
respect to this basis. For each n-tuple
(v1,..., vn) we
consider the geodesic
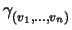 (t) (upto some order
in t) obtained as above, starting at p and proceeding along
(t) (upto some order
in t) obtained as above, starting at p and proceeding along
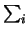 viei. One easily sees that the functions
viei. One easily sees that the functions
ui(
v1,...,
vn) =
ui(
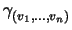
(1))
give another parametric form (in the variables v1,...,vn) for
the manfiold M (upto some order r). This form is called the
geodesic normal form for M. We can re-express any function on M in
terms of the new variables by substitution. Similarly, we can compute
the speed of curves
(v1(t),..., vn(t) in terms of a new matrix
(Gij) which can easily be computed in terms of the gij and
the expression of u's as functions of v's.
It is clear that this special parametric form should reflect the
geometry of M. In fact, Riemman proved
Theorem 2
If the manifold
M is expressed in the variables
(
v1,...
vn) in
geodesic normal form, and the expression for spped of a curve takes
the form
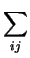 Gijvi, tvj, t
Gijvi, tvj, t =
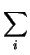 vi, t2
vi, t2 +
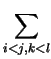 cij, kl
cij, kl(
vivj, t -
vjvi, t)(
vkvl, t -
vlvk, t)
modulo order 3 terms in the variables
vi.
The second term can be thought of as a quadratic form
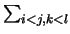 cij, klzijzkl in a new set of variables zij. By
diagonalising this quadratic form as earlier we obtain n(n - 1)/2
``eigenvalues'' which are called the principal sectional
curvatures of M in analogy with the two dimensional case given in
the exercise above. Many interesting properties of curvature have been
developed over the years. Riemann himself showed that the curvature is
0 at all points of M if and only if M is Euclidean. He also
claimed that the functions on M given by the principal sectional
curvatures uniquely determine the geometry of M. This claim has only
been proved partially.
cij, klzijzkl in a new set of variables zij. By
diagonalising this quadratic form as earlier we obtain n(n - 1)/2
``eigenvalues'' which are called the principal sectional
curvatures of M in analogy with the two dimensional case given in
the exercise above. Many interesting properties of curvature have been
developed over the years. Riemann himself showed that the curvature is
0 at all points of M if and only if M is Euclidean. He also
claimed that the functions on M given by the principal sectional
curvatures uniquely determine the geometry of M. This claim has only
been proved partially.



Next: Suggested Reading
Up: Coordinate Geometry
Previous: Surfaces
Kapil H. Paranjape
2001-01-20
![]() k are
k are
![]() and hence the
acceleration of a curve on M can be computed one we are given the
gij as functions of ui. We no longer need the ``crutch'' of
the vector-valued functions x(ui). Thus, the geometry of the
manifold M is entirely described by the matrix-valued function
(gij) with values in positive-definite matrices. This function
gives the speed of a curve (ui(t)) as
and hence the
acceleration of a curve on M can be computed one we are given the
gij as functions of ui. We no longer need the ``crutch'' of
the vector-valued functions x(ui). Thus, the geometry of the
manifold M is entirely described by the matrix-valued function
(gij) with values in positive-definite matrices. This function
gives the speed of a curve (ui(t)) as
![]() gijui, tuj, t and the accleration is given by the formula above.
gijui, tuj, t and the accleration is given by the formula above.
![]()
![]() ui, tuj, t + uk, tt = 0, we can
inductively solve for ui, 2, ui, 3 and so on.
ui, tuj, t + uk, tt = 0, we can
inductively solve for ui, 2, ui, 3 and so on.
![]() (t) (upto some order
in t) obtained as above, starting at p and proceeding along
(t) (upto some order
in t) obtained as above, starting at p and proceeding along
![]() viei. One easily sees that the functions
viei. One easily sees that the functions
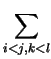 cij, kl(vivj, t - vjvi, t)(vkvl, t - vlvk, t)
cij, kl(vivj, t - vjvi, t)(vkvl, t - vlvk, t)