


Next: Bibliography
Up: Some Lectures on Number
Previous: A..1 Counterexample
In order to compare the given definition of schemes with the
``classical'' one, we will prove the following theorem:
Theorem 18
Let
f :
R S
S be a homomorphism between finitely generated rings so
that for every finite ring
A, the induced map
Hom(
S,
A)

Hom(
R,
A) is a bijection. Then
f is an isomorphism.
In the paragraphs below R and S will always denote rings
satisfying the conditions of the theorem. We first prove a special
case:
Lemma 19
Let
f :
R S
S be a homomorphism of finite rings so that for every
finite ring
A the induced map
Hom(
S,
A)

Hom(
R,
A) is a
bijection. Then
f is an isomorphism.
Proof.
Taking
A =
R we see that there is a homomorphism
g :
S R
R such
that the composite
gof :
R S
S R
R is identity. For any
finite ring
A, consider the chain of maps
Hom(
R,
A)
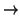
Hom(
S,
A)
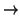
Hom(
R,
A)
The second map is a bijection by assumption. The composite is the
identity and in particular, a bijection. It follows that
Hom(
R,
A)

Hom(
S,
A) is a bijection as well. Now, taking
A =
S we
see that we also have a homomorphism
h :
R S
S so that the
composite homomorphism
S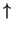 gR
gR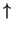 hS
hS is the identity. We then
have
f = idSof = hogof = hoidR = h
Thus
fog = id
S and
gof = id
R, hence
f and
g are
isomorphisms.
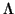
Next, we show that the above condition is ``inherited'' by quotients.
Lemma 20
Let
f :
R S
S be as above. Let
I be an ideal in
R, then we
obtain a homomorphism
R/
I S
S/
f (
I)
S. For any finite ring
A, the
induced map
Hom(
S/
f (
I)
S,
A)

Hom(
R/
I,
A) is a bijection.
Proof.
Consider the diagram
| Hom(S, A) |
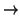 |
Hom(R, A) |
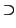 |
|
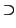 |
| Hom(S/f (I)S, A) |
|
Hom(R/I, A) |
The top row is a bijection. Let
g :
S/
f (
I)
S A
A be any element in
the bottom left corner then the corresponding element
h :
S A
A in
the top left corner satisfies
h(
f (
I)
S) = 0. Thus
hof :
R A
A
satisfies
hof (
I) = 0. Thus it factors through a homomorphism
e :
R/
I A
A. Thus we see that the elements in the bottom left
corner are mapped to elements in the bottom right corner.
Conversely, let
g :
R/
I A
A be an element in the bottom right
corner and
h :
R A
A be its image in the top right corner; then
h(
I) = 0. By assumption there is a homomorphism
e :
S A
A such that
h =
eof. It follows
e(
f (
I)) = 0 and thus
e(
f (
I)
S) = 0. Thus
e
factors through an element
d :
S/
f (
I)
S A
A in the bottom left
corner. In other words we have a bijection
Hom(
S/
f (
I)
S,
A)

Hom(
R/
I,
A).
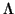
Combining the above two lemmas we see that if I is any ideal in
R such that R/I and S/f (I)S are finite, then the map
R/I S/f (I)S is an isomorphism. We will now show that if R/I is finite
then S/f (I)S is ``automatically'' finite as well.
S/f (I)S is an isomorphism. We will now show that if R/I is finite
then S/f (I)S is ``automatically'' finite as well.
Lemma 21
Let
f :
R S
S be as in the theorem. For any maximal ideal
m in
R, the ideal
f (
m)
S in
S also a maximal ideal.
Proof.
Since
R is finitely generated
R/
m is a finite field by Hilbert's
Nullstellensatz. Thus
Hom(
S,
R/
m)

Hom(
R,
R/
m) is a bijection and
so the homomorphism
R R
R/
m must factor through
S; moreover,
this factorisation is unique. Let
n be the kernel of this
factorisation. Then
n is a maximal ideal containing
f (
m)
S such
that
R/
m S
S/
n is an isomorphism. Now, let
n' be any maximal
ideal in
S containing
f (
m)
S. Then, the composite
R S
S S
S/
n' factors through
R/
m. Thus,
S/
n' is a finite field
extension of
R/
m. If this extension has degree > 1 then if
q is
the cardinality of
R/
m, the map
x 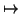 xq
xq is a non-trivial
automorphism of
S/
n' which is identity on
R/
m. Thus we obtain
two maps
S S
S/
n' which restrict to the same map
R S
S/
n'
contradicting the hypothesis. Thus
R/
m S
S/
n' is an isomorphism.
But then this isomorphism gives a map
S R
R/
m which restricts to
the natural map
R R
R/
m; there is a unique such map by
hypothesis. Since that map has kernel
n, we see that
n' =
n.
In other words, we see that f (m)S is contained in a unique maximal
ideal n in S. Thus S/f (m)S is an Artinian ring. By the earlier
discussion we see that
R/m S/f (m)S is an isomorphism. In other
words f (m)S = n is a maximal ideal for every maximal ideal m in
R. Conversely, if n is any maximal ideal in S, then
f-1(n) = m is the kernel of the composite
R
S/f (m)S is an isomorphism. In other
words f (m)S = n is a maximal ideal for every maximal ideal m in
R. Conversely, if n is any maximal ideal in S, then
f-1(n) = m is the kernel of the composite
R S
S S/n which
is a map to a finite field; hence m is a maximal ideal. It follows
that every maximal ideal in S is of the form f (m)S for a
maximal ideal m in R.
S/n which
is a map to a finite field; hence m is a maximal ideal. It follows
that every maximal ideal in S is of the form f (m)S for a
maximal ideal m in R.
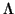
Now, if I is any ideal such that R/I is finite then there are
finitely many maximal ideals m1, ..., mk and positive integers
r1, ..., rk such that
I 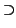 m1r1 . m2r2 ... mkrk. As seen above
ni = f (mi)S is a
maximal ideal. The relations
m1r1 . m2r2 ... mkrk. As seen above
ni = f (mi)S is a
maximal ideal. The relations
f (
I)
S  f
f (
m1r1 ... mkrk)
S =
n1r1 ... nkrk
shows that the ring S/f (I)S is finite as well. It follows that for
any ideal I such that R/I is finite, the map
R/I S/f (I)S is
an isomorphism.
S/f (I)S is
an isomorphism.
On the other hand suppose J is any ideal in S such that S/J is
finite and let
I = f-1(J); then R/I is a subring of S/J and
thus also finite. We have seen above that this implies that
R/I S/f (I)S is an isomorphism. But the inverse image of J/f (I)S under
this is the zero ideal in R/I. Thus we have J = f (I)S. To
summarise,
S/f (I)S is an isomorphism. But the inverse image of J/f (I)S under
this is the zero ideal in R/I. Thus we have J = f (I)S. To
summarise,
Lemma 22
Let
f :
R S
S be as in the conditions of the theorem. The map
I 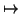 f
f (
I)
S is a one-one correspondence between ideals of
finite index in
R and ideals of finite index in
S. The map
J 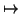 f-1
f-1(
J) is the inverse correspondence from ideals
J
in
S to ideals in
R. Moreover, the natural homomorphism
R/
I S
S/
f (
I)
S is an isomorphism for such ideals.
Thus the original condition has been re-stated intrinsically in terms
of ideals. Next we wish to prove that the given homomorphism is
``closed''. That is to say given a prime ideal Q in S, let
m be a maximal ideal in R that contains the prime ideal
P = f-1(Q). We wish to prove that there is a maximal
ideal n in S which contains Q and satisfies
f-1(n) = m.
To do this we can restrict our attention to
R/P S/f (Q)S. Since
f-1(f (P)S)
S/f (Q)S. Since
f-1(f (P)S) 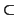 f-1(Q) = P, the latter homomorphism is also injective.
f-1(Q) = P, the latter homomorphism is also injective.
Lemma 23
Let
f :
R S
S be an injective homomorphism of finitely generated
rings with
R a domain. We have a factoring of
f as follows
R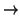 R
R[
X1,...,
Xa] =
R1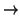 R1
R1[
t1,...,
tb] =
R2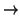 S
S
where
- R1 is a polynomial ring over R.
- There is a non-zero element r of R1 such that for each
i, the element
rti
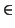 R2 satisfies a monic polynomial over
R1. Other than this relation there are no further relations
among the ti in R2.
R2 satisfies a monic polynomial over
R1. Other than this relation there are no further relations
among the ti in R2.
- R2
 S is the quotient by an ideal that intersects R1
in the zero ideal.
S is the quotient by an ideal that intersects R1
in the zero ideal.
Proof.
Since
S is finitely generated we can choose a maximal collection
of elements
X1, ...,
Xa of
S that are algebraically
independent over (the quotient field of)
R. Then
R1 =
R[
X1,...,
Xa] is the polynomial ring over
R and is a
subring of
S. The remaining generators of
S are algebraically
dependent on the
Xi's. Thus each of them satisfies an equation of
the form
r0Td +
r1Td - 1 + ... +
rd for some elements
rj in
R1. Moreover, we can assume that
r0 is non-zero in such an
equation. Let
r be the product in
R1 of polynomials
r0
corresponding to different generators of
S. Since
R is a
domain, so is
R1 and the polynomial
r is non-zero. For each
generator
S choose a polynomial of the above form with leading
coefficient
r (one such such clearly exists) and let
R2 be the
ring obtained from
R1 by adjoining the roots of these equations.
We have a natural map
R2 S
S; let
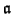
be the kernel. Since
R1 S
S factors through
R2 and is injective, it follows that
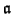
intersects
R1 in the zero ideal.
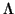
Let Q1, ..., Qr be the minimal primes in S or equivalently a
minimal primes in R2 that contains the kernel of R2 S. Since
R1 meets this kernel in the zero ideal, the intersection of the
prime ideals
Qi
S. Since
R1 meets this kernel in the zero ideal, the intersection of the
prime ideals
Qi 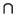 R1 in R1 is a nilpotent ideal. Since R1
is a domain there is an index i such that
Qi
R1 in R1 is a nilpotent ideal. Since R1
is a domain there is an index i such that
Qi 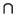 R1 = (0). Let Q
denote the prime ideal Qi for any such index i.
R1 = (0). Let Q
denote the prime ideal Qi for any such index i.
Let m be a maximal ideal in R such that r is not contained in
the prime ideal
m[X1,..., Xa] of R1. Since R1 is a domain
we see that
Qr 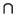 (R1)r is the zero ideal. Now, (R2)r is a
finite free module over (R1)r and so (by the going up theorem)
there is a prime ideal Q' in R2 which contains Q and restricts
to
m[X1,..., Xa] in R1. Similarly, for any maximal ideal n'
in R1 that contains
m[X1,..., Xa] and does not contain r,
there is a maximal ideal n in R2 that contains Q' (and hence
Q) that lies over n'.
(R1)r is the zero ideal. Now, (R2)r is a
finite free module over (R1)r and so (by the going up theorem)
there is a prime ideal Q' in R2 which contains Q and restricts
to
m[X1,..., Xa] in R1. Similarly, for any maximal ideal n'
in R1 that contains
m[X1,..., Xa] and does not contain r,
there is a maximal ideal n in R2 that contains Q' (and hence
Q) that lies over n'.
Now, if a > 0 (i. e. R 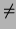 R1) then there are at least two (in
fact infinitely many) such maximal ideals n'. But then we see that
we have at least two maximal ideals in S that lie over a given
maximal ideal m in R contradicting lemma 22. Thus we must
have R = R1.
R1) then there are at least two (in
fact infinitely many) such maximal ideals n'. But then we see that
we have at least two maximal ideals in S that lie over a given
maximal ideal m in R contradicting lemma 22. Thus we must
have R = R1.
Again, if 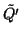 is another minimal prime in R2 that contains
the kernel of R2
is another minimal prime in R2 that contains
the kernel of R2 S and such that
S and such that
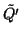
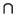 R1 = (0), then
as above we can find a prime ideal
R1 = (0), then
as above we can find a prime ideal
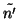 which contains
which contains
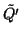 and lies over m and is distinct from Q'. Now there are
distinct maximal ideals n' and
and lies over m and is distinct from Q'. Now there are
distinct maximal ideals n' and
 in R2, that contain
Q' and
in R2, that contain
Q' and
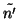 respectively. This again contradicts
lemma 22. It follows that there is a unique minimal
prime Q containing the kernel of R2
respectively. This again contradicts
lemma 22. It follows that there is a unique minimal
prime Q containing the kernel of R2 S such that
Q
S such that
Q 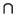 R = (0).
R = (0).
Now suppose that Q0 is another miminal prime in S, or
equivalently a minimal prime in R2 that contains the kernel of
R2 S. We must have
Q0
S. We must have
Q0 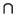 R
R 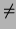 (0). However, we have the
lemma
(0). However, we have the
lemma
Lemma 24
Let
f :
R S
S be a homomorphism of finitely generated rings with
R a domain. Let
Q be a minimal prime in
S such that
f-1(
Q) is non-zero. Then there is a maximal ideal
n in
S
and an integer
k such that if
m =
f-1(
n), then
R/
mk S
S/
nk
is not an isomorphism.
Proof.
Let
x be an element of all the minimal primes of
S other than
Q. Replacing
S by its localisation
Sx at
x, we can
assume that
Q is the unique minimal prime in
S. Then
Q consists of nilpotent elements. Since
f-1(
Q) is
non-zero and
R is a domain it follows that
R S
S has a non-zero
kernel. Now let
n be
any maximal ideal in
S and
m =
f-1(
m). The homomorphism of local rings
Rm Sn
Sn has a
non-zero kernel. The result follows by the Artin-Rees lemma.
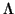
On the other hand, for our given homomorphism R S we know that
R/mk
S we know that
R/mk S/nk must be an isomorphism for all k. It follows that
there is no such prime ideal Q0 in S.
S/nk must be an isomorphism for all k. It follows that
there is no such prime ideal Q0 in S.
We have thus proved that there is a unique prime ideal Q in S that
lies over a given prime ideal P in R and
f-1(Q) = P. The
``closed''-ness condition is an immediate corollary.
Let us note that if R[X] is the polynomial ring over a ring R,
then
Hom(R[X], A) is naturally identified with
Hom(R, A)×A. Thus, if
g : R[X] S[X] denotes the natural extension of the
above homomorphism to the corresponding polynomial rings then, for any
finite ring the induced map
Hom(S[X], A)
S[X] denotes the natural extension of the
above homomorphism to the corresponding polynomial rings then, for any
finite ring the induced map
Hom(S[X], A) Hom(R[X], A) is a
bijection whenever
Hom(S, A)
Hom(R[X], A) is a
bijection whenever
Hom(S, A) Hom(R, A) is a bijection. In
particular, we can apply the above lemmas to the homomorphism g as
well.
Hom(R, A) is a bijection. In
particular, we can apply the above lemmas to the homomorphism g as
well.
Lemma 25
Let
f :
R S
S be as in the theorem and
g :
R[
X]
 S
S[
X] be the
induced homomorphism on polynomial rings in one variable. Let
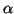
be any element of
S and
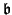
be the ideal
(
X -
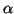
)
S[
X] in
S[
X]. Let
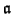
be the ideal
g-1((
X -
a)
S[
X]). Then
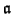
contains a
monic
polynomial.
Proof.
Let
A be any ring and
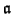
be an ideal in the polynomial ring
A[
X]. Let
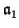
denote the ideal
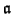 . A
. A[
X,
X-1]
in the ring
A[
X,
X-1]. We have
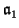
= {
P(
X)
. X-n|
P(
X)
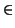
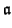
and
n 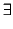
0 an integer }
Let
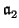
be the restriction
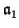
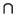 A
A[
X-1] of this
ideal to
A[
X-1]. We have
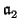
= {
P(
X)
. X-d|
P(
X)
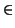
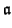
and
d = deg(
P(
X))}
The
content
c(
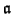
) of the ideal
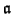
is defined as
the image of
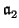
in
A[
X-1]/(
X-1) =
A. Clearly,
c(
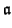
) = {
a 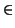 A
A|
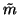 P
P(
X)
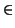
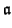
such that
P(
X) =
aXd + lower degree terms }
Returning to the rings
R and
S let us use the subscripts 1 and 2
to denote the above constructions applied to ideals in
R[
X] and
S[
X]; specifically to the ideals
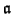
and
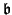
.
We want to show that the content
c(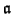 ) of the ideal
) of the ideal
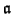 in R[X] is the unit ideal. Suppose that
c(
in R[X] is the unit ideal. Suppose that
c(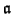 )
) 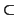 m for
some maximal ideal m in R. The ideal
m for
some maximal ideal m in R. The ideal
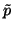 = m[X-1] + X-1R[X-1] is then a maximal ideal in
R[X-1] which contains
= m[X-1] + X-1R[X-1] is then a maximal ideal in
R[X-1] which contains
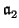 . Moreover, by the above
description of
. Moreover, by the above
description of
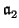 it is clear that
it is clear that
 = g2-1(
= g2-1(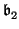 ), where
g2 : R[X-1]
), where
g2 : R[X-1] S[X-1] is
the natural homomorphism. Applying the ``going-up'' which has been
proved above, it follows that there should exist a prime ideal
S[X-1] is
the natural homomorphism. Applying the ``going-up'' which has been
proved above, it follows that there should exist a prime ideal
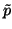 containing
containing
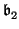 such that
g2-1(
such that
g2-1(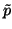 ) =
) = 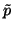 . But
. But
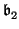 is the ideal
generated by
1 -
is the ideal
generated by
1 - 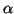 X-1 and X-1 lies in
X-1 and X-1 lies in
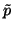 . Thus
. Thus 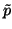 would have to be the unit ideal which
contradicts its primality. It follows that
c(
would have to be the unit ideal which
contradicts its primality. It follows that
c(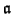 ) is the unit
ideal.
) is the unit
ideal.
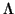
From this lemma we see that S is integral over R. Now the
result that
R/m S/f (m)S is an isomorphism for all maximal ideals
m implies theorem 18 by Nakayama's lemma.
S/f (m)S is an isomorphism for all maximal ideals
m implies theorem 18 by Nakayama's lemma.



Next: Bibliography
Up: Some Lectures on Number
Previous: A..1 Counterexample
Kapil Hari Paranjape
2002-10-20
![]() S/f (m)S is an isomorphism. In other
words f (m)S = n is a maximal ideal for every maximal ideal m in
R. Conversely, if n is any maximal ideal in S, then
f-1(n) = m is the kernel of the composite
R
S/f (m)S is an isomorphism. In other
words f (m)S = n is a maximal ideal for every maximal ideal m in
R. Conversely, if n is any maximal ideal in S, then
f-1(n) = m is the kernel of the composite
R![]() S
S![]() S/n which
is a map to a finite field; hence m is a maximal ideal. It follows
that every maximal ideal in S is of the form f (m)S for a
maximal ideal m in R.
S/n which
is a map to a finite field; hence m is a maximal ideal. It follows
that every maximal ideal in S is of the form f (m)S for a
maximal ideal m in R.
![]()
![]() S/f (I)S is an isomorphism. But the inverse image of J/f (I)S under
this is the zero ideal in R/I. Thus we have J = f (I)S. To
summarise,
S/f (I)S is an isomorphism. But the inverse image of J/f (I)S under
this is the zero ideal in R/I. Thus we have J = f (I)S. To
summarise,
![]() (R1)r is the zero ideal. Now, (R2)r is a
finite free module over (R1)r and so (by the going up theorem)
there is a prime ideal Q' in R2 which contains Q and restricts
to
m[X1,..., Xa] in R1. Similarly, for any maximal ideal n'
in R1 that contains
m[X1,..., Xa] and does not contain r,
there is a maximal ideal n in R2 that contains Q' (and hence
Q) that lies over n'.
(R1)r is the zero ideal. Now, (R2)r is a
finite free module over (R1)r and so (by the going up theorem)
there is a prime ideal Q' in R2 which contains Q and restricts
to
m[X1,..., Xa] in R1. Similarly, for any maximal ideal n'
in R1 that contains
m[X1,..., Xa] and does not contain r,
there is a maximal ideal n in R2 that contains Q' (and hence
Q) that lies over n'.
![]() R1) then there are at least two (in
fact infinitely many) such maximal ideals n'. But then we see that
we have at least two maximal ideals in S that lie over a given
maximal ideal m in R contradicting lemma 22. Thus we must
have R = R1.
R1) then there are at least two (in
fact infinitely many) such maximal ideals n'. But then we see that
we have at least two maximal ideals in S that lie over a given
maximal ideal m in R contradicting lemma 22. Thus we must
have R = R1.
![]() is another minimal prime in R2 that contains
the kernel of R2
is another minimal prime in R2 that contains
the kernel of R2![]() S and such that
S and such that
![]()
![]() R1 = (0), then
as above we can find a prime ideal
R1 = (0), then
as above we can find a prime ideal
![]() which contains
which contains
![]() and lies over m and is distinct from Q'. Now there are
distinct maximal ideals n' and
and lies over m and is distinct from Q'. Now there are
distinct maximal ideals n' and
![]() in R2, that contain
Q' and
in R2, that contain
Q' and
![]() respectively. This again contradicts
lemma 22. It follows that there is a unique minimal
prime Q containing the kernel of R2
respectively. This again contradicts
lemma 22. It follows that there is a unique minimal
prime Q containing the kernel of R2![]() S such that
Q
S such that
Q ![]() R = (0).
R = (0).
![]() S. We must have
Q0
S. We must have
Q0 ![]() R
R ![]() (0). However, we have the
lemma
(0). However, we have the
lemma
![]() S[X] denotes the natural extension of the
above homomorphism to the corresponding polynomial rings then, for any
finite ring the induced map
Hom(S[X], A)
S[X] denotes the natural extension of the
above homomorphism to the corresponding polynomial rings then, for any
finite ring the induced map
Hom(S[X], A)![]() Hom(R[X], A) is a
bijection whenever
Hom(S, A)
Hom(R[X], A) is a
bijection whenever
Hom(S, A)![]() Hom(R, A) is a bijection. In
particular, we can apply the above lemmas to the homomorphism g as
well.
Hom(R, A) is a bijection. In
particular, we can apply the above lemmas to the homomorphism g as
well.
![]() ) of the ideal
) of the ideal
![]() in R[X] is the unit ideal. Suppose that
c(
in R[X] is the unit ideal. Suppose that
c(![]() )
) ![]() m for
some maximal ideal m in R. The ideal
m for
some maximal ideal m in R. The ideal
![]() = m[X-1] + X-1R[X-1] is then a maximal ideal in
R[X-1] which contains
= m[X-1] + X-1R[X-1] is then a maximal ideal in
R[X-1] which contains
![]() . Moreover, by the above
description of
. Moreover, by the above
description of
![]() it is clear that
it is clear that
![]() = g2-1(
= g2-1(![]() ), where
g2 : R[X-1]
), where
g2 : R[X-1]![]() S[X-1] is
the natural homomorphism. Applying the ``going-up'' which has been
proved above, it follows that there should exist a prime ideal
S[X-1] is
the natural homomorphism. Applying the ``going-up'' which has been
proved above, it follows that there should exist a prime ideal
![]() containing
containing
![]() such that
g2-1(
such that
g2-1(![]() ) =
) = ![]() . But
. But
![]() is the ideal
generated by
1 -
is the ideal
generated by
1 - ![]() X-1 and X-1 lies in
X-1 and X-1 lies in
![]() . Thus
. Thus ![]() would have to be the unit ideal which
contradicts its primality. It follows that
c(
would have to be the unit ideal which
contradicts its primality. It follows that
c(![]() ) is the unit
ideal.
) is the unit
ideal.
![]()