


Next: B. Comparison with ``classical''
Up: A. A missing Lemma
Previous: A. A missing Lemma
Let R be a subring of a number field K and suppose that R is
finitely generated as an abelian group. Let
(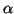 ,
,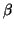 ) = Trace(
) = Trace(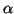
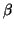 ) denote the non-degenerate
symmetric form on K as above. Also let
) denote the non-degenerate
symmetric form on K as above. Also let 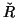 be the collection
of elements
be the collection
of elements 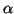 in K such that
(
in K such that
(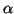 , R)
, R) 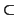
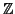 . Now
let
. Now
let 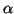 be any element of K such that
be any element of K such that
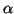
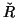
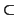
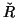 . Then we have
(
. Then we have
(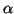 ,
,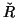 )
) 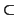
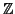 . By the non-degeneracy of the pairing
we see that
. By the non-degeneracy of the pairing
we see that 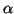 lies in R. Thus by putting
M =
lies in R. Thus by putting
M = 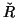 we see
that R is precisely the ring associated by M in the leading
paragraph of this section. Thus to provide a counterexample to the
stated result it is enough to show that there is an R such that
we see
that R is precisely the ring associated by M in the leading
paragraph of this section. Thus to provide a counterexample to the
stated result it is enough to show that there is an R such that
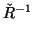 .
. 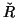 is strictly smaller than R.
is strictly smaller than R.
Let b be an integer which is not a cube. Let K be the field obtain
by adjoining a cube root 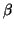 of b to
of b to
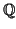 . Let a be any
non-zero integer and let R be the subring of K generated by
w1 = 1,
w2 = a
. Let a be any
non-zero integer and let R be the subring of K generated by
w1 = 1,
w2 = a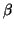 and
w3 = a
and
w3 = a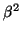 . We have the identities
. We have the identities
w12 = w1;w1w2 = w2;w1w3 = w3;w22 = aw3;w2w3 = a2b;w32 = abw1
It follows that
Trace(w1) = 3 and
Trace(w1) = Trace(w2) = 0.
Thus if
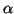 = a1w1 + a2w2 + a3w3 is such that
(
= a1w1 + a2w2 + a3w3 is such that
(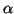 , R)
, R) 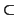
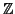 we obtain the conditions
Thus a basis for
we obtain the conditions
Thus a basis for 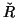 is given by u1 = w1/3,
u2 = w2/(3a2b) and
u3 = w3/(3a2b). Now suppose that
is given by u1 = w1/3,
u2 = w2/(3a2b) and
u3 = w3/(3a2b). Now suppose that
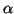 = a1w1 + a2w2 + a3w3 is such that
= a1w1 + a2w2 + a3w3 is such that
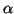
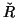
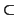 R. We obtain the conditions
R. We obtain the conditions
a1 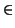
3
a2b . 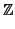
;
a2 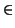
3
ab . 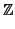
;
a3 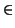
3
a . 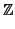
;
A basis for
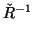 is thus given by
v1 = 3a2bw1,
v2 = 3abw2 and v3 = 3aw3. We then compute
is thus given by
v1 = 3a2bw1,
v2 = 3abw2 and v3 = 3aw3. We then compute
u1v1 = a2bw1;u2v3 = aw1;u3v2 = abw1
It follows that aw1 is in the product
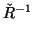 .
. 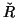 but w1 is not. Hence the product is
strictly smaller than R.
but w1 is not. Hence the product is
strictly smaller than R.



Next: B. Comparison with ``classical''
Up: A. A missing Lemma
Previous: A. A missing Lemma
Kapil Hari Paranjape
2002-10-20
![]() of b to
of b to
![]() . Let a be any
non-zero integer and let R be the subring of K generated by
w1 = 1,
w2 = a
. Let a be any
non-zero integer and let R be the subring of K generated by
w1 = 1,
w2 = a![]() and
w3 = a
and
w3 = a![]() . We have the identities
. We have the identities