


Next: 9.3 Divisors
Up: 9 Hyperelliptic Cryptosystems
Previous: 9.1 Hyperelliptic curves
A proper closed reduced irreducible subscheme of T (or
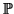 1) is
called a closed point. Let P be a closed point of T and Q
be its image in
1) is
called a closed point. Let P be a closed point of T and Q
be its image in
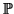 1. If U, V denote the coordinates on
1. If U, V denote the coordinates on
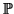 1 then Q is defined as the vanishing locus of an irreducible
homogeneous polynomial F(U, V). Thus either F = V and Q is the
point at infinity on
1 then Q is defined as the vanishing locus of an irreducible
homogeneous polynomial F(U, V). Thus either F = V and Q is the
point at infinity on
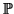 1 or V does not divide F. In the
latter case Q is contained in
1 or V does not divide F. In the
latter case Q is contained in
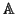 1 which is the open subset of
1 which is the open subset of
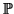 1 where V is a unit (i. e. the complement of the point at
infinity). The coordinate on
1 where V is a unit (i. e. the complement of the point at
infinity). The coordinate on
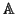 1 is given by x = U/V and Q
defined by the irreducible polynomial
f (x) = F(U, V)/Vdeg(F). Now,
if Q is the point at infinity then the description in the previous
paragraph shows that P must be the point at infinity on T. In the
second case P is an irreducible closed subscheme of the subscheme of
1 is given by x = U/V and Q
defined by the irreducible polynomial
f (x) = F(U, V)/Vdeg(F). Now,
if Q is the point at infinity then the description in the previous
paragraph shows that P must be the point at infinity on T. In the
second case P is an irreducible closed subscheme of the subscheme of
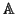 2 defined by the equations
2 defined by the equations
| y2 + a(x)y + b(x) |
= |
0 |
|
| f (x) |
= |
0 |
|
In other words, let
E = 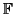 [x]/(f (x)) be the finite extension of the
ground field
[x]/(f (x)) be the finite extension of the
ground field
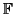 and let
and let 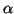 and
and 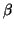 be the images of a(x)
and b(x) in E. The closed point P is given by solving the
equation
y2 +
be the images of a(x)
and b(x) in E. The closed point P is given by solving the
equation
y2 + 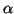 y +
y + 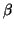 over E. Clearly, there are three cases
to consider. The case when this equation has multiple roots (when
over E. Clearly, there are three cases
to consider. The case when this equation has multiple roots (when
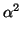 - 4
- 4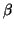 = 0) is clear the case which corresponds to
Weierstrass points. The case when this equation is irreducible over
E is the case case when P is the full inverse image of Q under
the morphism
T
= 0) is clear the case which corresponds to
Weierstrass points. The case when this equation is irreducible over
E is the case case when P is the full inverse image of Q under
the morphism
T
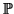 1. Finally, when the quadratic equation is
solvable in E, there is an element
1. Finally, when the quadratic equation is
solvable in E, there is an element 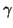 in E that corresponds
to the point P. Now
in E that corresponds
to the point P. Now 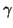 is the image in E of a polynomial
g(x) in
is the image in E of a polynomial
g(x) in
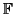 [x], we can further choose g so that its degree is less
than the degree of f. To summarise, a closed point of T takes one
of the following forms:
[x], we can further choose g so that its degree is less
than the degree of f. To summarise, a closed point of T takes one
of the following forms:
- The point at infinity on T.
- An irreducible factor f (x) of the discriminant
a(x)-4b(x)
is given. In this case there is a unique polynomial g(x) of degree
less than deg(f ) so that y = g(x) represents the (unique)
solution of the equation
y2 + a(x)y + b(x) in the field
E =
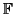 [x]/(f (x)).
[x]/(f (x)).
- We have an irreducible polynomial f that is co-prime to the
discriminant and the quadratic equation
y2 + a(x)y + b(x) is
irreducible modulo f (x).
- We have an irreducible polynomial f (x) that is co-prime to the
discriminant. Moreover, we are given a polynomial g(x) of degree
less than deg(f ) so that y = g(x) represents one of the two
solutions of the equation
y2 + a(x)y + b(x) in the field
E =
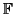 [x]/(f (x)).
[x]/(f (x)).
We note that the first two cases above correspond to Weierstrass
points on T.
One should not be misled by the term ``closed point''--when
considering solutions over general finite rings (in our case rings
that are finite dimensional vector spaces over
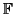 suffice), we can
find that each closed point has many ``elements''. In fact, let
suffice), we can
find that each closed point has many ``elements''. In fact, let
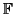 (P)
denote the field
E =
(P)
denote the field
E = 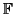 [x]/(f (x)) in cases (2) and (4). In case (3) let
[x]/(f (x)) in cases (2) and (4). In case (3) let
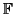 (P) be the quadratic extension of E where the irreducible
quadratic polynomial
y2 +
(P) be the quadratic extension of E where the irreducible
quadratic polynomial
y2 + 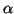 y +
y + 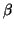 has its roots. We note that
has its roots. We note that
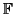 (P) is a finite extension of the finite field
(P) is a finite extension of the finite field
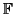 and hence is a
Galois extension; thus it contains all the roots of any
polynomial which has one of root in it. From this one sees that
P(
and hence is a
Galois extension; thus it contains all the roots of any
polynomial which has one of root in it. From this one sees that
P(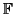 (P)) is a finite set of cardinality equal to the degree
[
(P)) is a finite set of cardinality equal to the degree
[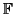 (P) :
(P) : 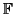 ]; note that this is deg(f ) in cases (2) and (4) and is
2 deg(f ) in case (3). This number
]; note that this is deg(f ) in cases (2) and (4) and is
2 deg(f ) in case (3). This number
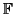 (P) : P] is called the degree of the closed point P and denoted deg(P).
(P) : P] is called the degree of the closed point P and denoted deg(P).



Next: 9.3 Divisors
Up: 9 Hyperelliptic Cryptosystems
Previous: 9.1 Hyperelliptic curves
Kapil Hari Paranjape
2002-10-20
![]() suffice), we can
find that each closed point has many ``elements''. In fact, let
suffice), we can
find that each closed point has many ``elements''. In fact, let
![]() (P)
denote the field
E =
(P)
denote the field
E = ![]() [x]/(f (x)) in cases (2) and (4). In case (3) let
[x]/(f (x)) in cases (2) and (4). In case (3) let
![]() (P) be the quadratic extension of E where the irreducible
quadratic polynomial
y2 +
(P) be the quadratic extension of E where the irreducible
quadratic polynomial
y2 + ![]() y +
y + ![]() has its roots. We note that
has its roots. We note that
![]() (P) is a finite extension of the finite field
(P) is a finite extension of the finite field
![]() and hence is a
Galois extension; thus it contains all the roots of any
polynomial which has one of root in it. From this one sees that
P(
and hence is a
Galois extension; thus it contains all the roots of any
polynomial which has one of root in it. From this one sees that
P(![]() (P)) is a finite set of cardinality equal to the degree
[
(P)) is a finite set of cardinality equal to the degree
[![]() (P) :
(P) : ![]() ]; note that this is deg(f ) in cases (2) and (4) and is
2 deg(f ) in case (3). This number
]; note that this is deg(f ) in cases (2) and (4) and is
2 deg(f ) in case (3). This number
![]() (P) : P] is called the degree of the closed point P and denoted deg(P).
(P) : P] is called the degree of the closed point P and denoted deg(P).