


Next: 9.2 Closed points
Up: 9 Hyperelliptic Cryptosystems
Previous: 9 Hyperelliptic Cryptosystems
Loosely speaking, hyperelliptic curves represent the solutions of the
equations of the form
y2 + a(x)y + b(x) = 0
where a and b are polynomials in x. To put this in the language
of schemes developed earlier, we first restrict our attention to
schemes over
Spec(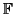 ) where
) where
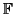 is a finite field called the ground field. Next we consider the d - tuple Veronese embedding of
is a finite field called the ground field. Next we consider the d - tuple Veronese embedding of
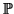 1 in
1 in
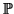 d; also known as the ``rational normal curve of
degree d''; this is given as the locus of
(1 : x : x2 : ... : xd) as
(1 : x) varies over
d; also known as the ``rational normal curve of
degree d''; this is given as the locus of
(1 : x : x2 : ... : xd) as
(1 : x) varies over
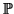 1. Alternatively, it is described by the
system of equations
XpXq = XrXs for all p, q, r, s such
that p + q = r + s. Let us consider
1. Alternatively, it is described by the
system of equations
XpXq = XrXs for all p, q, r, s such
that p + q = r + s. Let us consider
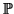 d + 1 with
(X0 : ... : Xd : Y)
as its co-ordinates so that
d + 1 with
(X0 : ... : Xd : Y)
as its co-ordinates so that
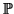 d is obtained by projecting from
the point (vertex)
v = (0 : ... : 0 : 1). Let Sd denote the ``cone''
over the rational normal curve of degree d; it is the subvariety of
d is obtained by projecting from
the point (vertex)
v = (0 : ... : 0 : 1). Let Sd denote the ``cone''
over the rational normal curve of degree d; it is the subvariety of
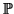 d defined by the same set of equations as above (in other words
the variable Y is ``free''). Now suppose that
a(x) =
d defined by the same set of equations as above (in other words
the variable Y is ``free''). Now suppose that
a(x) = 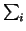 aixi
is a polynomial of degree at most d and
b(x) =
aixi
is a polynomial of degree at most d and
b(x) = 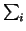 bixi is a
polynomial of degree at most 2d. We consider the linear forms
bixi is a
polynomial of degree at most 2d. We consider the linear forms
| A(X) |
= |
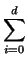 aiXi aiXi |
|
| B(X) |
= |
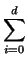 biXi biXi |
|
| C(X) |
= |
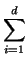 bd + iXi bd + iXi |
|
and the quadratic equation
Y2 + A(X)Y + B(X)X0 + C(X)Xd = 0. The addition
of this equation to the equations for S defines a subvariety T of
S. It is clear that the vertex v does not lie on T so that
projection gives a morphism on T which lands in the rational normal
curve of degree d. Thus, we have a morphism
T
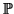 1. There is
an involution on
1. There is
an involution on
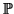 d + 1 which fixes the X's and sends Y to
A(X) - Y. Clearly this involution
d + 1 which fixes the X's and sends Y to
A(X) - Y. Clearly this involution 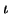 sends T to itself and
pairs of points that are involutes of each other are sent to the same
point in
sends T to itself and
pairs of points that are involutes of each other are sent to the same
point in
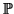 1. The variety T is called a hyperelliptic curve,
the involution is called the hyperelliptic involution and the morphism
T
1. The variety T is called a hyperelliptic curve,
the involution is called the hyperelliptic involution and the morphism
T
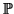 1 is called the canonical morphism.
1 is called the canonical morphism.
Now it is clear that a solution (x, y) of the equation
y2 + a(X)y + b(x) = 0 gives rise to the solution
(1 : x : ... : xd : y) of
the above system. Conversely, if we have a solution
(X0 : X1 : ... : Xd : Y) of the system of equations with X0 a unit,
then we can put
(x, y) = (X1/X0, Y/X0) to obtain a solution of the
two variable equation. Similarly, if
(X0 : ... : Xd : Y) is a
solution of the system of equations and Xd is a unit then consider
the pair
(u, v) = (Xd - 1/Xd, Y/Xd); this pair satisfies a two
variable equation
v2 + a'(u)v + b'(u) = 0, where
a'(u) = uda(1/u) and
b'(u) = u2db(1/u). One sees from the above system that either X0
or Xd must be a unit so we have covered all cases. The Jacobian
criterion for regularity can be used to show that the curve defined by
y2 + a(x)y + b(x) = 0 is regular when either,
- the discriminant
a(x)2 - 4b(x) has distinct roots, or
- the field
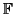 has characteristic 2, a(x) has distinct roots
and for each point (x0, y0) where x0 is a root of a(x), the
polynomial
b(x) - b(x0) - y0a(x) vanishes with multiplicity one at
0.
has characteristic 2, a(x) has distinct roots
and for each point (x0, y0) where x0 is a root of a(x), the
polynomial
b(x) - b(x0) - y0a(x) vanishes with multiplicity one at
0.
To apply this to the equation
v2 + a'(u)v + b'(u) = 0, we note that
a'(u)2 - 4b'(u) = u2d(a(1/u)2 - 4b(1/u))
Thus, if
a(x)2 - 4b(x) has distinct roots, then the only multiple
root of
a'(u)2 - 4(b'(u) can be at u = 0; moreover, this happens only
if a(x) has degree less than d - 1 and b(x) has degree less than
2d - 1. From now one we will assume the T is regular or
non-singular; in fact we will assume that b(x) has degree equal to 2d - 1. The point
(0 : ... : 0 : 1 : 0) is a point on the
curve T is called the ``point at infinity'' and denoted 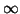 .
The number g = d - 1 is called the genus of the hyperelliptic curve. The
points on T where
a(x)2 - 4b(x) vanishes and the point at infinity
are called the Weierstrass points of the hyperelliptic curve;
these are precisely the fixed points of the Weierstrass involution.
.
The number g = d - 1 is called the genus of the hyperelliptic curve. The
points on T where
a(x)2 - 4b(x) vanishes and the point at infinity
are called the Weierstrass points of the hyperelliptic curve;
these are precisely the fixed points of the Weierstrass involution.



Next: 9.2 Closed points
Up: 9 Hyperelliptic Cryptosystems
Previous: 9 Hyperelliptic Cryptosystems
Kapil Hari Paranjape
2002-10-20