


Next: 1.1 Addition and Subtraction
Up: Some Lectures on Number
Previous: Some Lectures on Number
We need to go back to school and remember how we did basic arithmetic!
Recall that we first learnt how to operate with small numbers i. e. the digits. Then we learnt how to represent and manipulate bigger
numbers. Thus for us ``human''-sized symbols are the symbols 0-9 which
we consider ``small''; in a similar way the numbers 0-232 - 1 or the
numbers made (in base 2) of thirty-two 0's and 1's are ``small'' for a
computer. We must already know the following operations with these
numbers; we use W to denote the set of basic symbols which represent
natural numbers from 0 to M - 1 (M = 10 for humans and M = 232 for
computers):
- addition
- The operation of addition with carry
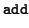
:
W×
W×{0, 1}
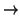 W
W×{0, 1}
where
(a, b,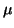 )
) 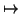 (c,
(c,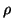 ) which satisfies
) which satisfies
a +
b +
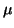
=
c +
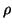 . M
. M
- subtraction
- The operation of subtraction with borrow
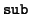
:
W×
W×{0, 1}
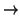 W
W×{0, 1}
where
(a, b,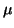 )
) 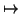 (c,
(c,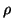 ) which satisfies
) which satisfies
a -
b -
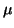
=
c -
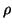 . M
. M
- multiplication
- The operation of multiplication with
remainder
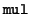
:
W×
W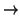 W
W×
W
where
(a, b)  (c, d ) which satisfies
(c, d ) which satisfies
a . b = c . M + d
- division
- The operation of division with
remainder (this is a partial function)
:
W×
W×
W W
W×
W
where
(a, b, c)  (d, e) when b < a and satisfies
(d, e) when b < a and satisfies
b . M + c = a . d + e
with e < a.
There may be some further operations that we may need to check
whether on element of W is less than another or equal to another and
so on.
The main aim of this section is to write down methods of computing
with integers written in the ``usual'' way as strings of symbols
u1u2 ... up representing
u1 . Mp - 1 + ... + u1. We
will also count the number of steps taken to make our calculations
under the assumption that each of the above operations counts as one
step.
Subsections



Next: 1.1 Addition and Subtraction
Up: Some Lectures on Number
Previous: Some Lectures on Number
Kapil Hari Paranjape
2002-10-20
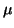 = c +
= c + 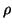 . M
. M
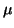 = c -
= c - 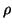 . M
. M