


Next: 1.5 Faster Algorithms
Up: 1 Multiple Precision Arithmetic
Previous: 1.3 Long Division Algorithm
So far we have been discussing things in generalities but when we make
some assumptions about the machine then the above algorithms can be
improved or simplified. For example, in the first algorithm for
division, when M = bn and there is a ``left shift'' operation on the
symbol that amounts to multiplication by b, it is quicker to
multiply iteratively by b to get something close enough to the
required d. In this case division by d in the last step is also
replaced by an appropriate ``right shift''.
On the other hand no such simplification is possible in the second
algorithm for division, but (as is often true about ``real'' machines)
if 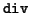 is a significantly slower operation than the others, then
it may be worthwhile to perform the extra steps.
is a significantly slower operation than the others, then
it may be worthwhile to perform the extra steps.
Since most of our operations are on binary computers (so that
M = 2n), we have special procedures to multiply and divide by powers
of 2. We now describe these procedures based on some new fundamental
operations.
- left shift
- The operation of multiplication by a power of 2
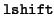
:
W×{0,...,
n - 1}
 W
W×
W
where
(a, k)  (c, d ) which satisfies
(c, d ) which satisfies
2k . a = c . M + d
- right shift
- The operation of division by a power of 2
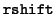
:
W×{0,...,
n - 1}
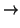 W
W×
W
where
(a, k) 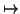 (c, d ) which satisfies
(c, d ) which satisfies
a . M/2k = c . M + d
- zero
- The operation of finding out whether something is
non-zero; this is also the ``bit-wise and'' operation

:
W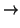
{0, 1}
where
a 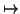 0 if a is zero and 1 if it is non-zero.
0 if a is zero and 1 if it is non-zero.
- bitwise negation
- The difference from M - 1; this is also
the operation of bitwise negation
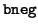
:
W W
W
where
a 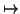 M - a - 1.
M - a - 1.
- integer log to the base 2
- The operation of finding the
integer part of the logarithm to base 2
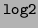
:
W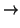
{0,...,
n - 1}
where
a 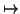 k which satisfies
2k
k which satisfies
2k 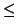 a < 2k. This also
counts the number of right shifts possible without carry.
a < 2k. This also
counts the number of right shifts possible without carry.
- left shift count
- The number of left shifts possible without carry.
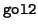
:
W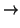
{0,...,
n - 1}
where
a 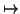 k which satisfies
M/2
k which satisfies
M/2 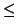 2ka < M.
2ka < M.
We can use these operations to produce some special algorithms. We
note that we have already used the
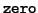 operation without mention!
operation without mention!
Given a small integer k and an integer
(u1 ... uq), we can
construct
(v0 ... vq) satisfying
(v0 ... vq) = 2k ... (u0 ... vq) as follows.
We compute
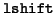 (ui, k) = (si - 1, ti),
(ui, k) = (si - 1, ti),
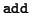 (si, ti, 0) = (vi, 0) and
v0 = s0. Similarly, we can easily compute division by 2k. We can
also find the precise power of 2 that divides any integer
(u1 ... uq) (also called the 2-adic value of this integer). Clearly all
these operations are of order linear in q. We can further extend
this procedure quite easily to integers
(k1 ... kr) of size r
with only r extra steps (to divide k by M).
(si, ti, 0) = (vi, 0) and
v0 = s0. Similarly, we can easily compute division by 2k. We can
also find the precise power of 2 that divides any integer
(u1 ... uq) (also called the 2-adic value of this integer). Clearly all
these operations are of order linear in q. We can further extend
this procedure quite easily to integers
(k1 ... kr) of size r
with only r extra steps (to divide k by M).
Finally, we can also use the given basic operations to implement
comparisons between integers which are linear in the size of the
integers concerned.
We summarise our investigations in the following table
| Operation |
Time taken |
| Addition/Subtraction |
Linear |
| Multiplication/Division by small integers |
Linear |
| Multiplication/Division |
Quadratic |
| Multiplication/Division by powers of 2 |
Linear |
| Comparison |
Linear |
| 2-adic value |
Linear |
Beyond this point we will not refer to the basic operations like
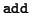 any more and make use of the higher level operations on
integers mentioned above. If we do find a need for some specialised
higher level operations to be implemented faster we should come back
here and add to this section rather than complicate later sections!
any more and make use of the higher level operations on
integers mentioned above. If we do find a need for some specialised
higher level operations to be implemented faster we should come back
here and add to this section rather than complicate later sections!



Next: 1.5 Faster Algorithms
Up: 1 Multiple Precision Arithmetic
Previous: 1.3 Long Division Algorithm
Kapil Hari Paranjape
2002-10-20
![]() is a significantly slower operation than the others, then
it may be worthwhile to perform the extra steps.
is a significantly slower operation than the others, then
it may be worthwhile to perform the extra steps.
![]() (ui, k) = (si - 1, ti),
(ui, k) = (si - 1, ti),
![]() (si, ti, 0) = (vi, 0) and
v0 = s0. Similarly, we can easily compute division by 2k. We can
also find the precise power of 2 that divides any integer
(u1 ... uq) (also called the 2-adic value of this integer). Clearly all
these operations are of order linear in q. We can further extend
this procedure quite easily to integers
(k1 ... kr) of size r
with only r extra steps (to divide k by M).
(si, ti, 0) = (vi, 0) and
v0 = s0. Similarly, we can easily compute division by 2k. We can
also find the precise power of 2 that divides any integer
(u1 ... uq) (also called the 2-adic value of this integer). Clearly all
these operations are of order linear in q. We can further extend
this procedure quite easily to integers
(k1 ... kr) of size r
with only r extra steps (to divide k by M).