


Next: 1.2 Multiplication Algorithm
Up: 1 Multiple Precision Arithmetic
Previous: 1 Multiple Precision Arithmetic
We now write the addition recipe using the usual method
| |
u1 |
u2 |
... |
up |
| |
v1 |
v2 |
... |
vp |
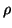 |
w1 |
w2 |
... |
wp |
Or more concisely
(
u1 ... up) + (
v1 ... vp) = (
w1 ... wp) +
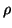 Mp
Mp = (
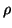 w1 ... wp
w1 ... wp)
(wp,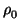 ) ) |
= |
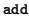 (up, vp, 0) (up, vp, 0) |
|
(wp - i,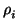 ) ) |
= |
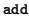 (up - i, vp - i, (up - i, vp - i,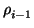 ) ) |
|
We can clearly write these identities quite concisely by defining
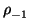 = 0. It is thus clear how to calculate this
inductively for all i upto i = p. At the last stage the carry over
is the extra
= 0. It is thus clear how to calculate this
inductively for all i upto i = p. At the last stage the carry over
is the extra
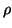 =
= 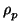 in the answer.
in the answer.
A similar technique applies to the subtraction method. We write the
identity
(
u1 ... up) - (
v1 ... vp) = (
w1 ... wp) -
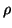 Mp
Mp
(wp,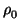 ) ) |
= |
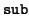 (up, vp, 0) (up, vp, 0) |
|
(wp - i,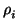 ) ) |
= |
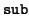 (up - i, vp - i, (up - i, vp - i,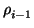 ) ) |
|
Again, putting
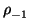 = 0 combines the identities and we can easily
compute these inductively. Note that
= 0 combines the identities and we can easily
compute these inductively. Note that
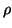 =
= 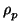 is the ``extra''
borrow element and so if this is non-zero then
(v1 ... vp) is in
fact more than
(u1 ... up). We will see that this calculation is
useful even in this case.
is the ``extra''
borrow element and so if this is non-zero then
(v1 ... vp) is in
fact more than
(u1 ... up). We will see that this calculation is
useful even in this case.
We note that the number of steps taken by both methods is equal to p.



Next: 1.2 Multiplication Algorithm
Up: 1 Multiple Precision Arithmetic
Previous: 1 Multiple Precision Arithmetic
Kapil Hari Paranjape
2002-10-20