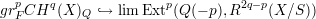11. Motives
The theory of Motives was proposed by Grothendieck as an ideal cohomological
theory for varieties and schemes. Recent work by Levine, Suslin and Voevodsky
gives a construction of an almost final version of this theory. Another such
construction has been given by Nori. One problem is proving the equivalence of
these constructions. Another way of approaching this is to demonstrate the Hard
Lefschetz theorem for these theories.
A study of these and related problems has been undertaken by the author in
collaboration with G. Ravindra and Gautham Dayal (of the Chennai
Mathematical Institute).
Using Saito’s theory of Hodge Modules we are now able to combine the
arithmetic conjectures of Bloch and Beilinson with the analytic theory of cycles
to make the following unified conjecture. (Similar work has also been recently
done by Akasura and Saito independently).
Fix an embedding of Q the algebraic closure of Q, the field of rational numbers
into C the field of complex numbers. Let S be any variety over Q; Saito has
defined the category of Mixed Hodge Modules over S (actually, we will only be
concerned with a subcategory called the category of admissible variations of
mixed hodge structures). If 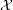 → S is an flat family, Saito constructs the Mixed
Hodge Modules Ri(X∕S) on S corresponding to the cohomologies of the fibres.
Now, if X is any variety over C, there is a filtered collection of families
→ S is an flat family, Saito constructs the Mixed
Hodge Modules Ri(X∕S) on S corresponding to the cohomologies of the fibres.
Now, if X is any variety over C, there is a filtered collection of families 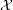 → S
so that X is its inverse limit. The arithmetic conjectures of Bloch and
Beilinson can now be formulated into a conjecture for varieties over C as
follows:
→ S
so that X is its inverse limit. The arithmetic conjectures of Bloch and
Beilinson can now be formulated into a conjecture for varieties over C as
follows:
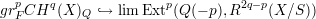
where the F denotes the filtration of Bloch on the Chow group, the limit is over
the above filtered collection and the Ext groups are in Satio’s mixed hodge
module category over S.
Finally, an important aspect of the the theory of motives is the construction of
concrete examples where this theory can be verified (in the absence of the
complete theory). We have constructed such typical examples and are in the
process of verifying all the predictions regarding algebraic cycles that are made
by the theory of motives in this cases. In particular, we are verifying that all
known examples of non-trivial cycles over C can be put in the framework of the
above conjecture. We have also constructed examples to show that conjectured
constructions of Ext2 due to M. Green are insufficient; this has already been
done earlier by C. Voisin but our examples are somewhat simpler than
hers.
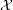 → S is an flat family, Saito constructs the Mixed
Hodge Modules Ri(X∕S) on S corresponding to the cohomologies of the fibres.
Now, if X is any variety over C, there is a filtered collection of families
→ S is an flat family, Saito constructs the Mixed
Hodge Modules Ri(X∕S) on S corresponding to the cohomologies of the fibres.
Now, if X is any variety over C, there is a filtered collection of families 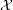 → S
so that X is its inverse limit. The arithmetic conjectures of Bloch and
Beilinson can now be formulated into a conjecture for varieties over C as
follows:
→ S
so that X is its inverse limit. The arithmetic conjectures of Bloch and
Beilinson can now be formulated into a conjecture for varieties over C as
follows: