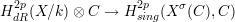8. Absolute Hodge cycles
Any projective variety X over the field of complex numbers C has as its field of
definition a finitely generated (over Q) subfield k. Let [Y ]  HdR2p(X∕k) be the
cycle class of a closed subvariety of X in the algebraic de Rham cohomology of X
over k (see [21] for a construction of such classes). Let σ : k
HdR2p(X∕k) be the
cycle class of a closed subvariety of X in the algebraic de Rham cohomology of X
over k (see [21] for a construction of such classes). Let σ : k C be any
embedding of k in the field of complex numbers. Under the comparison
isomorphism
C be any
embedding of k in the field of complex numbers. Under the comparison
isomorphism
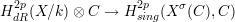
with (usual) singular cohomology, the class [Y ] maps to an integral class of type
(p,p). If one is to believe the Hodge conjecture then any integral class of type
(p,p) on Xσ must correspond to an algebraic cycle. It then follows that it must
be in the subset HdR2p(X∕k) and map to an integral class of type (p,p) under
any other embedding σ′. Even this (weak) consequence of the Hodge conjecture
is not known and led to the definition (see [6]) of an absolute Hodge
cycle.
In joint work with H. Esnault we explore the relation between this notion and
the notion of absolute de Rham cycle which we have introduced. The latter is an
infinitesimal analogue of the notion of absolute Hodge cycles and should prove
easier to study in relation with the Hodge conjecture.
In order to make the above work complete we needed a comparison theorem
between the Leray spectral sequence for algebraic de Rham cohomology and
singular cohomology. While proving this a number of other applications of these
homological tools were found. In particular, we were able to construct the
Leray spectral sequence for de Rham cohomology, prove the comparison
theorem with singular cohomology and also demonstrate the coniveau
spectral sequence used (without proof) in the paper ([1]) of Bloch and
Ogus.
 HdR2p(X∕k) be the
cycle class of a closed subvariety of X in the algebraic de Rham cohomology of X
over k (see [21] for a construction of such classes). Let σ : k
HdR2p(X∕k) be the
cycle class of a closed subvariety of X in the algebraic de Rham cohomology of X
over k (see [21] for a construction of such classes). Let σ : k C be any
embedding of k in the field of complex numbers. Under the comparison
isomorphism
C be any
embedding of k in the field of complex numbers. Under the comparison
isomorphism