Definitions

The study of differentiable functions is the study of functions that mimic the behaviour of polynomials ``approximately''. To begin with we must formally define the notion of approximation.

Exercise 34   For any real number 0 < x < 1 show that xⁿ is a decreasing sequence with limit 0.

In particular, we see that a polynomial that vanishes to order (n + 1) at 0 satisfies the following condition on functions of one variable.

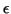
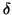
Definition 1   A function g(x) of one variable is said to be in o(xⁿ) if for any $\epsilon$ > 0 there is a $\delta$ > 0 so that

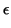
| g(x)| < $$\epsilon$$| xⁿ| for all x so that | x| < $$\delta$$.

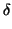
An alternative notion is

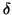
Definition 2   A function g(x) one variable is said to be in O(xⁿ) is there is a $\delta$ > 0 and a constant C so that

| g(x)| < C| xⁿ| for all x so that | x| < $$\delta$$

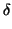
Clearly, any polynomial that vanishes to order n is O(xⁿ). Further, it is clear that an function g(x) that is O(xⁿ) is o(x^{n - 1}) and any function that is o(xⁿ) is O(xⁿ).

We can extend these notions to many variables as well. A function g(x₁,..., x_n) of n variables is said to be in o(xⁿ) (respectively O(xⁿ)) if for all lines (x₁,..., x_n) = (xc₁,..., xc_n) through the origin the restricted function f (x) = g(xc₁,..., xc_n) is in o(xⁿ) (respectively O(xⁿ)). We can further extend this to define o((x - b)ⁿ) and O((x - b)ⁿ) where b = (b₁,..., b_n) is some point, as a way of approximating functions near this point.

We say that g and f agree upto o((x - b)ⁿ) (or f approximates g upto o((x - b)ⁿ)) if f - g is in o((x - b)ⁿ). Note in particular, that f and g take the same value at b.

A function is differentiable n times at the point c if it is approximated upto o((x - b)ⁿ) by a polynomial (of degree n). Clearly, a polynomial of any degree is differentiable by the results of the previous section. In the one variable case we write this as follows

f (x) = a₀ + a₁x + ^... + a_nxⁿ + o((x - c)ⁿ)

Exercise 35   Show that for any two functions f and g in o(xⁿ) and a function h which is differentiable n times at the origin, the function h ^. f + g is in o(xⁿ).

Exercise 36   Show that the numbers a_k are uniquely determined by the function f.

Now the number a₁ depends on f and the point c. Now suppose that f is differentiable (1 times) at all points c so that it can be written as above near every point c. Then we can define the derived function f' by letting f'(c) = a₁ for each point c; the function f' is also called the derivative of f. Now it clear that if f is the function given by a polynomial P then f' is dP/dx. Thus we also use the notation df /dx for f'. We have the derivation property as well.

Exercise 37   If f, g and h are differentiable then so is hf + g and

$${\frac{d}{dx}}$$(hf + g) = $${\frac{dh}{dx}}$$f + h$${\frac{df}{dx}}$$ + $${\frac{dg}{dx}}$$

However, unlike the condition of vanishing to order n at c, the condition o((x - c)ⁿ) is not very well behaved.

Exercise 38   Show that f (x) = x²sin(1/x) is o(x) but the derivative of f' is not o(x⁰).

A function f (x) is called continuous at a point c if f (x) - f (c) is o(x - c) (i. e. it is differentiable 0 times!). It is called continuous it it has this property at all points. Thus we would like to study functions f which are differentiable and in addition the derivative f' is continuous. Such functions are provided by the fundamental theorem of calculus.