Next: Conic sections
Up: Pre-requisites
Previous: Pre-requisites
Let us assume that we have the usual axiomatic framework of Euclidean
geometry. We will show that the points on a line can be given
arithmetic operations and identified with the ``usual'' decimal
numbers. Moreover, we can introduce co-ordinates in space using the
Euclidean framework. One important thing to note is that use only the parallel postulate--congruence (hence distance and
angle) play no role in the introduction of co-ordinates.
We are given some gadget that can draw the line joining two
points and the line parallel to a given line through a point outside
it. Such a gadget is a ruler with a roller. (Alternatively you can use the xfig program).
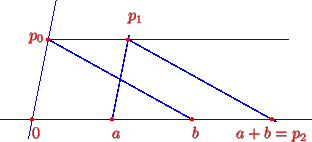
In the following constructions (see Figures 1 and 2)
we have numbered the lines and points in the sequence in which they
are obtained. Assume given a pair of points 0 and 1. We can define
addition and multiplication for points a and b on the line l
joining 0 and 1 by the constructions given below (the final point
in each construction is the sum or product of the the two original
points).
Exercise 1
Show that the following (usual) rules of arithmetic hold; in other
words the points on a line form a field.
- The commutative law for addition: a + b = b + a.
- The commutative law for multiplication: ab = ba.
- The associative law for addition:
(a + b) + c = a + (b + c).
- The associative law for multiplication:
a(bc) = (ab)c.
- The distributive law:
a(b + c) = ab + ac.
- The identity for addition: a + 0 = a.
- The identity for multiplication:
a . 1 = a.
- For any a there is a point (- a) so that a + (- a) = 0.
- For any non-zero a there is a point (1/a) so that a(1/a) = 1.
- If O' and 1' are two other points then give a natural
correspondence between the points of the line l' joining 0' and
1' and the line l so that the arithmetic structure is
preserved.
In addition, we can use the notion of order on the points of a line to
define an order in our arithmetic by saying that a number lies between
two other numbers if the corresponding points have the same relation.
In particular, we say that a > 0 if a is between the points 1
and 0 or if 1 is between a and 0 or if a is 1.
Exercise 2
Show in addition that
if a > 0 and b > 0 then a + b > 0 and
a . b > 0.
The following two important axioms are due to Archimedes (but only one
carries his name):
Axiom 1 (Also known as ``Big step - Little
step'')
If x > 0 (is a Little step) and y > 0 (is the Big step) then
there is a natural number n (the number of little steps) so that
y is less than nx.
The second axiom is perhaps even less ``obvious'' but is essential.
Axiom 2 (Least Upper Bound)
If
An is a sequence of points so
that for all
n,
An + 1 lies between
An and
D for some
fixed point
D (i. e.
An move towards
D but do not reach it).
Then there is a point
B which is the ``limit'' of
An. In other
words,
An + 1 is between
An and
B for all
n and if
C is
any other point so that
An + 1 lies between
An and
C then
B lies between
An and
C for all
n (see figure
3).
Figure 3:
The Least Upper Bound
|
|
Exercise 3
We introduce the decimal representation of a real number as
follows.
- Use the Archimedean Property to show that for any real number
x there is an integer n so that
n
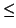 x < n + 1. This integer is
called the integer part [x] of x.
x < n + 1. This integer is
called the integer part [x] of x.
- Show that the sequence
xn = [10nx]/10n is a
non-decreasing sequence.
- Use the Least Upper Bound property to conclude that xn has a
limit y.
- Using the principle of the excluded middle show that y = x.
Finally, we choose four non-coplanar points in space and designate them
o, e1, e2 and e3. The point o is called the origin the
line through o and e1 (respectively e2 or e3) is called the
x-axis (respectively y-axis or z-axis). By drawing lines
parallel to the axes we can produce for any point a unique triple of points
(x, y, z) one on each axis which uniquely determine the point in space.
By the above method we obtain the co-ordinates in decimals as well.
Exercise 4
Show that a line in the plane is the locus of all points with
co-ordinates (x, y) such that ax + by + c = 0 for some constants a,
b and c so that a and b are not both zero. Also show the
converse.



Next: Conic sections
Up: Pre-requisites
Previous: Pre-requisites
Kapil H. Paranjape
2001-01-20