Next: Curves
Up: Coordinate Geometry
Previous: Coordinate Geometry
Conic sections are usually introduced as the first curves (as opposed
to lines) and are given as the locus of points satisfying an equation
of the form
ax2 + 2bxy + cy2 + 2dx + 2ey + f = 0
We have also studied that the behaviour of this equation is controlled
by the following determinants
D = det
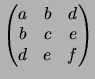
;
d = det
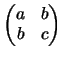
If D = 0 then the locus is a pair of lines which are parallel (and
could coincide) if d = 0. We get curves if D 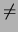 0 which are the
hyperbola, parabola and ellipse (or circle) if d is negative, zero
or positive (the circle corresponds to the latter when a = c). Since
we have defined addition and multiplication in geometric terms it
should not amaze us to see that the above definition can be made
without reference to an algebraic equation.
0 which are the
hyperbola, parabola and ellipse (or circle) if d is negative, zero
or positive (the circle corresponds to the latter when a = c). Since
we have defined addition and multiplication in geometric terms it
should not amaze us to see that the above definition can be made
without reference to an algebraic equation.
@fontpicture(6774,5871)(2239,-5965)
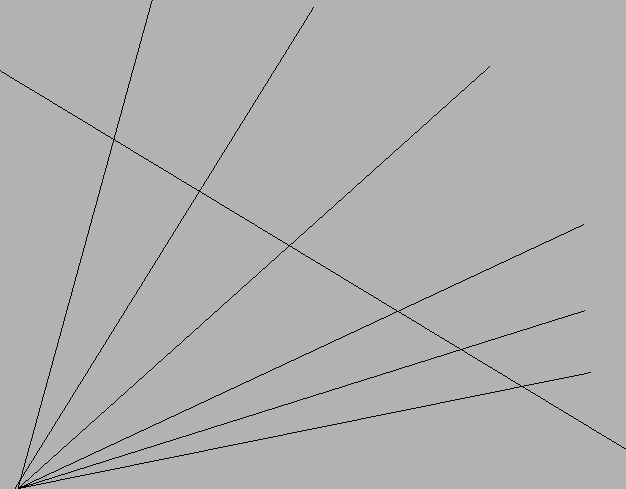
In order to understand this statement let us a fix a projective plane
and work within it. The collection of all lines through a fixed point
O are in natural 1-1 correspondence with the points on a line l
not containing O; any point B on l determines a unique line b
joining O and B and conversely, any line b through O meets l
in exactly one point B. The locus of lines through a fixed point is
called a pencil.
picture(6432,5758)(1036,-5639)
(1291,-5101)(0,0)[lb]O
(1246,-556)(0,0)[lb]l
(2296,-1216)(0,0)[lb]B
(2611,-46)(0,0)[lb]b
(1036,-5581)(0,0)[lb]The pencil of lines through a point O is in 1-1 correspondence with the points of l
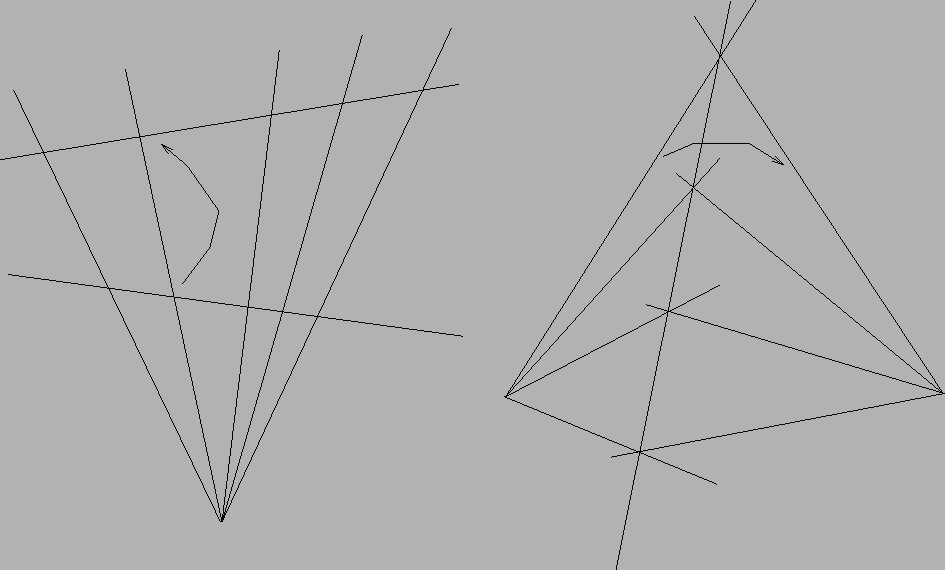
If l and m are two lines, neither containing a point O, then we have
natural correspondence given above between the points of each line and
the points of the pencil through O. This sets up a 1-1 correspondence
between the two lines. Explicitly, for each point A of l let a
be the line joining O and A and let B be the point of m that
lies on a. This correspondence is called the perspectivity
between the points of l and m with center O.
Similarly, if a pair of points A and B are such that neither lies
on a line l, then there is a natural 1-1 correspondence between the
pencils through A and B, since both the pencils have a 1-1
correspondence with the points of l. Explicitly, if p is a line
containing A which meets l in P, we consider the line q
joining B with P. This correspondence is called the perspectivity between the pencils through A and B with axis l.
picture(9414,6261)(154,-5650)
(6316,-5596)(0,0)[lb]Axial perspectivity between pencils
(5101,-3661)(0,0)[lb]A
(6166,-4876)(0,0)[lb]l
(9346,-3616)(0,0)[lb]B
(8506,-1576)(0,0)[lb]q
(6196,-1366)(0,0)[lb]p
(7471,-46)(0,0)[lb]P
(1501,-5581)(0,0)[lb]Central perspectivity between lines
(2161,-4921)(0,0)[lb]O
(211,-1186)(0,0)[lb]l
(286,-2446)(0,0)[lb]m
(1321,-766)(0,0)[lb]A
(1816,-1576)(0,0)[lb]a
(1711,-2536)(0,0)[lb]B
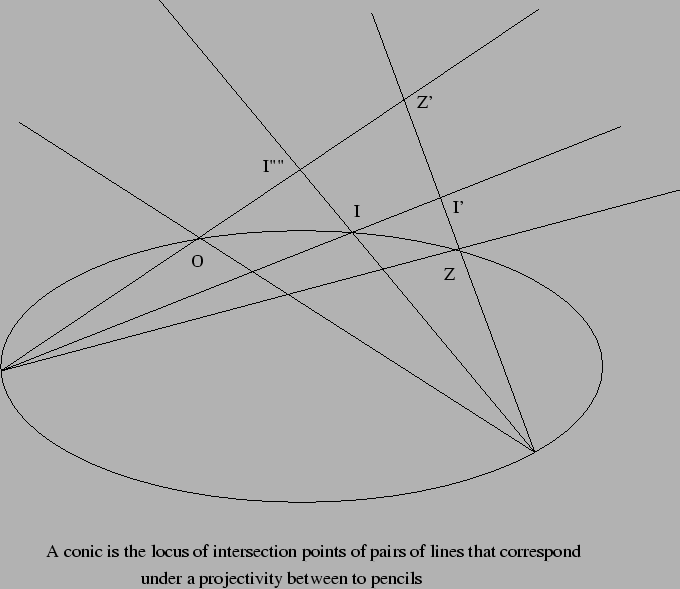
In both case a projective correspondence or projectivity
is defined as a composition of perspectivities. Thus, the
definition of a conic says, take a pair of points A and B and a
projectivity 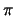 between the pencils of lines through A and B.
Let C be the locus of points of the form
l
between the pencils of lines through A and B.
Let C be the locus of points of the form
l 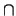
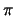 (l ) where l is
a line through A and
(l ) where l is
a line through A and 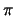 (l ) the corresponding line through B,
then C is a conic.
(l ) the corresponding line through B,
then C is a conic.
In order to understand projectivities better we note the following
Exercise 1
Given three points
O,
I and
Z one a line
l, and three points
O',
I',
Z' on a line
m. Each point
A other than the given
points on
l corresponds to an element
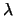
(
A) of
K - {0, 1}
where
K is the underlying field. Similarly, a point
B of
m other
than the given points corresponds to
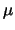
(
B) in
K - {0, 1}. A
perspectivity (and more generally a projectivity)
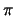
can be written
as
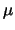
(
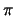
(
A)) = (
a +
b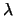
(
A))/(
c +
d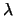
(
A)) where
a,
b,
c and
d are in
K and
ad -
bc 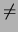
0.
picture(6729,5335)(1519,-4649)
(4756,-871)(0,0)[lb]I
(7456,-316)(0,0)[lb]Z
(2131,-3496)(0,0)[lb]O'
(2506,-1186)(0,0)[lb]O
(7111,-3931)(0,0)[lb]Z'
(4261,-3631)(0,0)[lb]I'
(3496,-2086)(0,0)[lb]I''
(7426,359)(0,0)[lb]A
(3031,-661)(0,0)[lb]B
(2011,-4591)(0,0)[lb]Central perspectivity from A and then B gives a general projectivity
The study of conics in projective geometry is a fascinating one but we
leave it here with a pointer to the suggested readings on projective
geometry. At the same time we note that it would be rather difficult
to study more complicated curves such as the locus of points
satisfying x3 + y3 = 1, using only the incidences between points and
lines and not algebra; this is possible in principle since the
addition and multiplication operations have been defined in terms of
the incidence relations. From now on we will use all the familiar
notions from algebra and deal with coordinate geometry.



Next: Curves
Up: Coordinate Geometry
Previous: Coordinate Geometry
Kapil H. Paranjape
2001-01-20
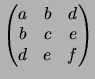 ; d = det
; d = det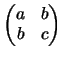
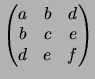 ; d = det
; d = det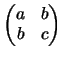

![]() between the pencils of lines through A and B.
Let C be the locus of points of the form
l
between the pencils of lines through A and B.
Let C be the locus of points of the form
l ![]()
![]() (l ) where l is
a line through A and
(l ) where l is
a line through A and ![]() (l ) the corresponding line through B,
then C is a conic.
(l ) the corresponding line through B,
then C is a conic.