11.6 Index calculus

Another useful tool goes by the name ``Index Calculus''. Suppose that we are given a set of generators g<sub>1</sub>, ..., g<sub>r</sub> of G and another ``black-box'' which computes a function A : G×R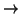$\to$$\mathbb {Z}$^r; here R is used to denote random input. The property of A is that given (g, k) (with k random) the output is an r-tuple (a₁,..., a_r), such that with probability greater than 1 - (1/2)^{r + t} (for some small integer t) we have the relation

g^k = 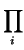$$\prod_{i}^{}$$g_i^a_i

(Note that one can quickly check whether this is indeed true). We can use such a black-box A to give a probabilistic solution to the group structure problem. By running the algorithm at most r + t times we will (with high probability) obtain sufficiently many relations to write g in terms of the elements g_i. 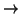Thus we can use this to construct a probabilistic algorithm that splits the map $\mathbb {Z}$^r$\to$G as required.

Since this algorithm makes use of one additional ``black-box'' it is not a ``generic group algorithm''.