


Next: 6 Algebraic Number Fields
Up: 5 Factorisation and Certificates
Previous: 5.2 Group theoretic method
We now examine the situation where N is almost certainly prime
(having passed the Miller-Rabin test many times with flying colors!).
In such a situation, we wish to provide a ``certificate'' that N is
a prime. In unison with Knuth, we could ask ``Why?''. After all, it is
really so highly improbable that N is not a prime that this is not
worth considering. One situation that one can think of is where an
``oracle'' produces keys for us. While we trust the oracle not to
``leak'' a key, we are not so sure that the oracle (in order to save
time and money) may be using some quick and dirty method to generate
the modulus, which may be weak. Then we would ask the oracle to
``provide proof'' that it has given us a prime number. Another
situation is that someone ``pays'' us to factor a number--we would
need to certify that the factorisation is complete. The certificate
should be very ``easy'' to check.
From this point of view, it is no use saying ``it passed the
Miller-Rabin test for me why don't you try it''. In fact (somewhat
more surprisingly perhaps) it is no use saying ``I have tried all
divisors upto 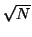 ''. Thus even if you are ``convinced'' that
you have a prime; how can you convince someone else without asking the
other person to perform an identical computation!
''. Thus even if you are ``convinced'' that
you have a prime; how can you convince someone else without asking the
other person to perform an identical computation!
Again group theoretic methods are very useful. In the situation of the
group scheme as above, suppose we find an non-trivial element g in
G(N) whose order m is larger than the order of G(p) for any
prime less than 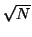 (recall that we have a good estimate of the
order of G(p)). Let d < m, then there is some ``co-ordinate'' of
gd which differs from the same coordinate for the identity element
of G; this is what one means by saying that gd is not the
identity element of G(N). Thus, this difference must be a unit of
(recall that we have a good estimate of the
order of G(p)). Let d < m, then there is some ``co-ordinate'' of
gd which differs from the same coordinate for the identity element
of G; this is what one means by saying that gd is not the
identity element of G(N). Thus, this difference must be a unit of
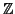 /N
/N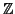 (since we are morally certain that N is a prime!). In
particular, for every prime factor q of m we provide a co-ordinate
of gm/q and its inverse xq in
(since we are morally certain that N is a prime!). In
particular, for every prime factor q of m we provide a co-ordinate
of gm/q and its inverse xq in
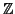 /N
/N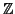 . This is a
certificate of primality.
. This is a
certificate of primality.
The person receiving this certificate would argue as follows. Suppose
p is the a prime factor of N that it is less than 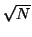 . Then
some power gd for d = m/q must become trivial in G(p) (since a
this group cannot have an element of order large than it!). But the
given co-ordinate of gd differs from the same co-ordinate of
identity by a unit in
. Then
some power gd for d = m/q must become trivial in G(p) (since a
this group cannot have an element of order large than it!). But the
given co-ordinate of gd differs from the same co-ordinate of
identity by a unit in
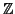 /N
/N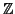 (we have given a proof of this by
providing xq). Thus this co-ordinate cannot be zero. Hence there
are not such prime prime factors--hence N is prime.
(we have given a proof of this by
providing xq). Thus this co-ordinate cannot be zero. Hence there
are not such prime prime factors--hence N is prime.
Thus a primality ``certificate'' would be the tuple
(G, g, m,{xq}q|). Of course, the correct-ness of this
certificate depends on the primality of various q's, so we would need a
certificate for those as well!
To make this explicit, suppose we find an element a in
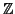 /N
/N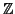 so that am = 1 but
am/q
so that am = 1 but
am/q 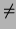 1 and
q
1 and
q 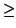
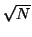 ; for some
integer m and a prime factor q. Then, N is prime; for if p is
a factor of N, then the
gcd(am/q - 1, p) divides
gcd(am/q - 1, N) and thus
am/q
; for some
integer m and a prime factor q. Then, N is prime; for if p is
a factor of N, then the
gcd(am/q - 1, p) divides
gcd(am/q - 1, N) and thus
am/q 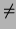 1 in
1 in
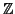 /p
/p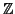 . But that
means q divides p - 1. On the other hand, if N is not prime, N
msut have a prime factor smaller than
. But that
means q divides p - 1. On the other hand, if N is not prime, N
msut have a prime factor smaller than 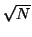 .
.
This can be carried some steps further.
Proposition 12
Suppose that
N - 1 =
f . r, where
f is completely factored into
primes
pi,
r has all its factors greater than
B and
gcd(
f,
r) = 1. Moreover, suppose that
f . B 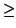
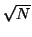
. Now
suppose that we find
ai so that its order is a multiple of the
exact power of
pi that divides
N - 1. Moreover, we have
b so
that
bN - 1 = 1 and
gcd(
bf - 1,
N) = 1, then
N is a prime.
Conversely, given such a factorisation of
N - 1, there are
a's as
required.
Proof.
Let
d be a prime divisor of
N. Then, the order of
ai in
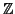
/
d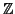
is divisible by exactly the same power of
pi that
divides
N - 1 (
gcd(
apiei - 1 - 1,
N) = 1 implies the same with
N replaced by
d). This means that
f divides
d - 1. Now, let
e be the order of
a0 in the units of
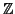
/
d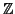
. Then
e
divides
d - 1 and
N - 1 =
f . r and does not divide
f = (
N - 1)/
r.
Thus
gcd(
e,
r) > 1. In particular,
gcd(
e,
u) >
B (since every prime
factor of
r has this property). Thus
gcd(
e,
u)
. f divides
d - 1, so that
d becomes larger than
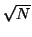
. But this cannot
be true for every prime factor of
N unless
N is
prime. (Exercise: find a more group-theoretic proof).
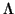
This can be used to provide a primality certificate as follows. We use
trial division upto a bound B0 to obtain a factorisation N - 1 = fr.
If
fB0 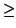
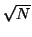 , then we take B = B0 and we are done. Otherwise
we check for the primality of r (say using the Miller-Rabin test).
If it is prime then we are done again (we have a complete
factorisation of F = N - 1). Otherwise we increase the bound B and
continue. The main problem (as usual) is with N - 1 having a few large
prime factors; in this case we would have to proceed to a bound B
like
, then we take B = B0 and we are done. Otherwise
we check for the primality of r (say using the Miller-Rabin test).
If it is prime then we are done again (we have a complete
factorisation of F = N - 1). Otherwise we increase the bound B and
continue. The main problem (as usual) is with N - 1 having a few large
prime factors; in this case we would have to proceed to a bound B
like 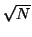 . As it turns out, once we have a factorisation of
N - 1, then we can proceed more surely, testing (in succession
aN - 1/q for each prime factor q of N - 1; if we fail for a given
a we can continue with the next a). One can show that the latter
will succeed quite quickly.
. As it turns out, once we have a factorisation of
N - 1, then we can proceed more surely, testing (in succession
aN - 1/q for each prime factor q of N - 1; if we fail for a given
a we can continue with the next a). One can show that the latter
will succeed quite quickly.
Lemma 13
Let q be a prime so that qf exactly divides the order of a
cyclic group G. The collection of elements, whose order is exactly
divisible by qe for e < f has cardinality at most 1/q times the
cardinality of G.
Thus the probability that a given element a will fail for all q is
the product of (1 - 1/q) which is very small. The proof of the lemma
is easy and left as an exercise.
As we can see the main stumbling block for this method is that we need
to factor N - 1 since the units in
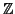 /N
/N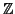 is the only
group available with us (so far) to apply this method to. Later we
will expand the class of groups (and so we can try to pick a
group with order easily factorisable) and it will be easier to find
such primality certificates.
is the only
group available with us (so far) to apply this method to. Later we
will expand the class of groups (and so we can try to pick a
group with order easily factorisable) and it will be easier to find
such primality certificates.



Next: 6 Algebraic Number Fields
Up: 5 Factorisation and Certificates
Previous: 5.2 Group theoretic method
Kapil Hari Paranjape
2002-10-20
![]() ''. Thus even if you are ``convinced'' that
you have a prime; how can you convince someone else without asking the
other person to perform an identical computation!
''. Thus even if you are ``convinced'' that
you have a prime; how can you convince someone else without asking the
other person to perform an identical computation!
![]() (recall that we have a good estimate of the
order of G(p)). Let d < m, then there is some ``co-ordinate'' of
gd which differs from the same coordinate for the identity element
of G; this is what one means by saying that gd is not the
identity element of G(N). Thus, this difference must be a unit of
(recall that we have a good estimate of the
order of G(p)). Let d < m, then there is some ``co-ordinate'' of
gd which differs from the same coordinate for the identity element
of G; this is what one means by saying that gd is not the
identity element of G(N). Thus, this difference must be a unit of
![]() /N
/N![]() (since we are morally certain that N is a prime!). In
particular, for every prime factor q of m we provide a co-ordinate
of gm/q and its inverse xq in
(since we are morally certain that N is a prime!). In
particular, for every prime factor q of m we provide a co-ordinate
of gm/q and its inverse xq in
![]() /N
/N![]() . This is a
certificate of primality.
. This is a
certificate of primality.
![]() . Then
some power gd for d = m/q must become trivial in G(p) (since a
this group cannot have an element of order large than it!). But the
given co-ordinate of gd differs from the same co-ordinate of
identity by a unit in
. Then
some power gd for d = m/q must become trivial in G(p) (since a
this group cannot have an element of order large than it!). But the
given co-ordinate of gd differs from the same co-ordinate of
identity by a unit in
![]() /N
/N![]() (we have given a proof of this by
providing xq). Thus this co-ordinate cannot be zero. Hence there
are not such prime prime factors--hence N is prime.
(we have given a proof of this by
providing xq). Thus this co-ordinate cannot be zero. Hence there
are not such prime prime factors--hence N is prime.
![]() /N
/N![]() so that am = 1 but
am/q
so that am = 1 but
am/q ![]() 1 and
q
1 and
q ![]()
![]() ; for some
integer m and a prime factor q. Then, N is prime; for if p is
a factor of N, then the
gcd(am/q - 1, p) divides
gcd(am/q - 1, N) and thus
am/q
; for some
integer m and a prime factor q. Then, N is prime; for if p is
a factor of N, then the
gcd(am/q - 1, p) divides
gcd(am/q - 1, N) and thus
am/q ![]() 1 in
1 in
![]() /p
/p![]() . But that
means q divides p - 1. On the other hand, if N is not prime, N
msut have a prime factor smaller than
. But that
means q divides p - 1. On the other hand, if N is not prime, N
msut have a prime factor smaller than ![]() .
.
![]() /N
/N![]() is the only
group available with us (so far) to apply this method to. Later we
will expand the class of groups (and so we can try to pick a
group with order easily factorisable) and it will be easier to find
such primality certificates.
is the only
group available with us (so far) to apply this method to. Later we
will expand the class of groups (and so we can try to pick a
group with order easily factorisable) and it will be easier to find
such primality certificates.