First of all let us follow Euclid's approach. Suppose a ![]() b. Let
u0 = (1, a) and v0 = (0, b). If b = 0, then our solution is
(x, z) = (1, a).
We compute, q0 = [a/b] (the integer part of a/b) and set
b. Let
u0 = (1, a) and v0 = (0, b). If b = 0, then our solution is
(x, z) = (1, a).
We compute, q0 = [a/b] (the integer part of a/b) and set
| v1 = (v1, 1, v1, 2) | = | u - q . v | |
| u1 = (u1, 1, u1, 2) | = | v |
| ui + 1 = (ui + 1, 1, ui + 1, 2) | = | vi | |
| vi + 1 = (vi + 1, 1, vi + 1, 2) | = | ui - qi . vi |
Extending Lehmer's approach is very similar. As above, suppose that
a ![]() b and let u0 = (1, a) and v0 = (1, b). We are at the step
i = 0. If vi, 2 = 0, then our solution is ui. Now let x denote
the leading ``digit'' of ui, 2 and y denote the leading digit
of vi, 2 at the same place (as in Lehmer's algorithm). We carry
through the process of Lehmer's algorithm to compute the matrix
b and let u0 = (1, a) and v0 = (1, b). We are at the step
i = 0. If vi, 2 = 0, then our solution is ui. Now let x denote
the leading ``digit'' of ui, 2 and y denote the leading digit
of vi, 2 at the same place (as in Lehmer's algorithm). We carry
through the process of Lehmer's algorithm to compute the matrix
![]()
![]()
![]() .
If B = 0 then we calculate
qi = [ui, 2/vi, 2] and set as above,
.
If B = 0 then we calculate
qi = [ui, 2/vi, 2] and set as above,
| ui + 1 = (ui + 1, 1, ui + 1, 2) | = | vi | |
| vi + 1 = (vi + 1, 1, vi + 1, 2) | = | ui - qi . vi |
| ui + 1 | = | Aui + Bvi | |
| vi + 1 | = | Cui + Dvi |
Finally, we turn to the binary GCD technique. As usual, if b is zero then we have the solution (x, y, z) = (1.0, a); if a is zero then we have the solution (x, y, z) = (0, 1, b). Otherwise, we take k to the minimum of the 2-adic values of a and b. Let c = a/2k and d = b/2k. Now, if d is even, then we interchange c and d and keep track of this interchange by setting a flag f to 1.
We may now assume that we have d odd and c non-zero. We will start with the pairs u1 = (1, c) and v1 = (0, d ) at i = 1. At each stage wi will be a pair in which the second part is even. Thus, if c is odd we put w1 = u1 - v1, else (if c is even) we put w1 = u1.
Now we perform the following steps inductively. First of all if wi, 2 = 0 then (x, z) = ui is the required pair and we exit the induction. Next we remove powers of two from wi. For this we take z1, i = wi and induct on zk, i as follows.
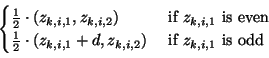
The last inductive step is the re-assignment. If zi, 2 is negative, then we take vi + 1 = - zi and ui + 1 = ui, otherwise we take ui + 1 = zi and vi + 1 = vi. Then we put wi + 1 = ui + 1 - vi + 1 and induct.
When we exit the induction, we have (x, z) so that d divides z - cx, so let y = z - cx/d. If f = 0, then we have ax + by = 2kz, while if f = 1 then we have ay + bx = 2kz. In both cases 2kz is the GCD of a and b (this follows since the steps that we are performing on the second part of the pairs ui and vi are exactly the same as those for binary GCD).