- ... steps1
- One thing that needs to be stated is that we are
repeatedly assigning values to variables. In the interests of
efficiency, any algorithm that deals with multi-precision arithmetic
should create new variables (allocate memory) and put values in them
infrequently. One way to do this is to decide in advance (by a
priori calculations) how many variables we will need and how
large they can get. Then we keep track of value variable ``names''
by means of a symmetric matrix (the number of variables is likely to
be much smaller than the numbers we are dealing with).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
enough2
- However, note that
x
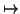 x2 - 2 is in fact a
powering map in disguise. If we put x = y + 1/y then this is the same
as
y
x2 - 2 is in fact a
powering map in disguise. If we put x = y + 1/y then this is the same
as
y 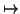 y2
y2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.