


Next: 4 The Proof of
Up: The Work of Efim
Previous: 2 Groups
For our purposes a p-group is a finite group such that it has pa
elements for some non-negative integer a. The Restricted Burnside
problem for such groups can be stated as follows.
Problem 4 (Restricted Burnside Problem for p-groups)
Let G be a finite group with exponent pn which is generated by k
elements. Then G has pa elements for some integer a. Is there a
uniform bound a(k, n) for a?
To study p-groups we first note that these are nilpotent.
We define the Central series for G
G1 = G and by induction on i, Gi = [G, Gi - 1]
Recall that G is nilpotent if Gi is the trivial group of
order 1 for some i. Now if G is a p-group then the abelian groups
Gi/Gi + 1 have order a power of p. Thus we can construct a finer
series called the p-Central series for G a p-group
G1 = G andGi + 1 is the subgroup generated by[G, Gi] and the setGip
By the above discussion it follows that Gi becomes trivial for
large enough i; in addition, each
Gi/Gi + 1 is a vector space
over
 Z/p
Z/p Z for all smaller i. The
Z for all smaller i. The
 Z/p
Z/p Z-vector space
L(G) is defined as
Z-vector space
L(G) is defined as
L(
G) =
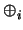 Gi
Gi/
Gi + 1
The non-commutative structure of G can be caught by a Lie algebra
structure on L(G). We recall the definition of a Lie algebra.
Definition 1
A vector space
L over a field
k is said to be a
lie algebra
if there is a pairing
[,] :
L×
L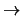 L
L with the following
properties
[x, y] = - [y, x] and [x,[y, z]] + [z,[x, y]] + [y,[z, x]] = 0
The Lie algebra structure on L(G) is given by
Gi/
Gi + 1×
Gj/
Gj + 1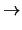 Gi + j
Gi + j/
Gi + j + 1
where the map is
(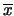 ,
,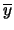 )
) 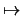
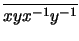 (Check
that this is well-defined!).
(Check
that this is well-defined!).
The above lie algebra has some additional structure. First is an
identity proved by Higman [7]. If G has exponent pn then
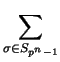
ad(
a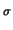 (1)
(1))
oad(
a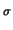 (2)
(2))
o ... oad(
a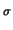 (pn - 1)
(pn - 1)) = 0
as a map
L(G)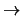 L(G); here
ad(a) : L
L(G); here
ad(a) : L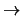 L for any element a in a
Lie algebra is the map
b
L for any element a in a
Lie algebra is the map
b 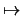 [a, b].
[a, b].
The second identity is proved by Sanov [11]. Let xi be the
elements of
G0/G1 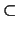 L(G) corresponding to the finitely many
generators gi of G. Then for any
L(G) corresponding to the finitely many
generators gi of G. Then for any 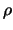 a commutator on the xi
we have
ad(
a commutator on the xi
we have
ad(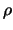 )pn = 0.
)pn = 0.
The main result of Zelmanov can formulated as follows.
Theorem 1 (Zelmanov)
Let
L be
any Lie algebra over
 Z
Z/
p Z
Z which is generated as
a Lie algebra by
k elements
xi such that we have the Higman and
Sanov identities.Then
L is nilpotent as a Lie algebra.
The interested reader can find this proof outlined in [13].



Next: 4 The Proof of
Up: The Work of Efim
Previous: 2 Groups
Kapil Hari Paranjape
2002-11-22
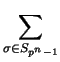 ad(a
ad(a![]() L(G) corresponding to the finitely many
generators gi of G. Then for any
L(G) corresponding to the finitely many
generators gi of G. Then for any ![]() a commutator on the xi
we have
ad(
a commutator on the xi
we have
ad(![]() )pn = 0.
)pn = 0.