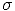
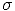 of k into the field of complex numbers
of k into the field of complex numbers  , the
, the  valued points of X
valued points of X 

 form
a complex manifold denoted by X
form
a complex manifold denoted by X . By base change for the de Rham cohomology
HDRj(X/k)
. By base change for the de Rham cohomology
HDRj(X/k) 

 = HDRj(X
= HDRj(X 

 /
/ ) and by the GAGA principle one has an isomorphism I
) and by the GAGA principle one has an isomorphism I from HDRj(X/k)
from HDRj(X/k) 

 to the Betti cohomology HBj(X
to the Betti cohomology HBj(X
 ,
, ) ([5], p. 96).
) ([5], p. 96).
 Chow group CHi(X)
Chow group CHi(X) 
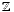
 has a de Rham class
has a de Rham class
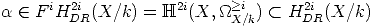
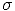 : k
: k 

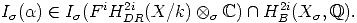
 is an absolute Hodge cycle, a notion defined by Deligne [3], §2, which we slightly
modify, as we are only interested here in de Rham cohomology (see [3], open question
2.2).
is an absolute Hodge cycle, a notion defined by Deligne [3], §2, which we slightly
modify, as we are only interested here in de Rham cohomology (see [3], open question
2.2).
Definition 1 A class 
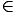 FiH
DR2i(X/k) is said to be an absolute Hodge cycle if for all
embeddings
FiH
DR2i(X/k) is said to be an absolute Hodge cycle if for all
embeddings 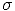 : k
: k 
 , I
, I (
( ) lies in HB2i(X
) lies in HB2i(X
 ,
, ).
).
On the other hand, such an algebraic cycle has an absolute de Rham class in 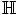 2i(X,
2i(X, 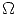 X/
X/ >i). In
fact, there is an absolute differential
>i). In
fact, there is an absolute differential
![dlog : O*X ----> _O_ >X1/Q [1]](ln2x.png)
![M >i
dlog : K i ----> _O_X/Q [i]](ln3x.png)

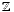
 = Hi(X,K
iM) ([9],
théorème 5), d log induces the absolute de Rham cycle class map
= Hi(X,K
iM) ([9],
théorème 5), d log induces the absolute de Rham cycle class map
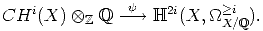
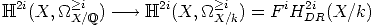


 = FiH
DR2i(X
= FiH
DR2i(X 

 /
/ ), so it is enough to handle
k =
), so it is enough to handle
k =  , in which case the compatibility is proven in [2], (2.2.5.1) and (2.2.5.2) for i = 1. For
i > 1, resolving the structure sheaf of an effective cycle by vector bundles, and for a given vector
bundle, computing its Chern classes on the Grassmannian bundle G
, in which case the compatibility is proven in [2], (2.2.5.1) and (2.2.5.2) for i = 1. For
i > 1, resolving the structure sheaf of an effective cycle by vector bundles, and for a given vector
bundle, computing its Chern classes on the Grassmannian bundle G 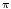 - -
- -  X, with
X, with
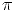 * : FiH
DR2i(X/
* : FiH
DR2i(X/ )
) FiH
DR2i(G/
FiH
DR2i(G/ ), one reduces the compatibility to the case
i = 1.
), one reduces the compatibility to the case
i = 1.
Remark 2 The existence of the absolute de Rham cycle class is proven in great generality in
[10] when X is singular. In fact, this class is convenient to formulate some questions. For
example, its injectivity for a surface X over k =  would imply Bloch’s conjecture when
H2(X,O
X) = 0.
would imply Bloch’s conjecture when
H2(X,O
X) = 0.
At any rate, the existence of 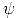 motivates the following
motivates the following
Definition 3 A class 
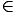 FiH
DR2i(X/k) is said to be an absolute de Rham cycle if it lies in the
image of HDR2i(X/
FiH
DR2i(X/k) is said to be an absolute de Rham cycle if it lies in the
image of HDR2i(X/ ) in
) in 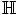 DR2i(X/k).
DR2i(X/k).
We denote by 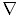 : HDRj(X/k)
: HDRj(X/k) 
 k/
k/ 1
1  kHDRj(X/k) the Gauss-Manin connection for the
smooth morphism X
kHDRj(X/k) the Gauss-Manin connection for the
smooth morphism X  Spec k of schemes over Spec
Spec k of schemes over Spec  .
.
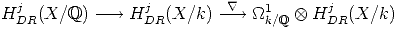
Proof. The sequence is obviously a complex.
Let k0  k be the field of definition of X. One has X = X0
k be the field of definition of X. One has X = X0  k0k, where X0 is smooth proper
over k0, and k0 =
k0k, where X0 is smooth proper
over k0, and k0 =  (S0) for a smooth affine variety S0 over
(S0) for a smooth affine variety S0 over  , such that there is a smooth
proper map f0 : X0
, such that there is a smooth
proper map f0 : X0  S0 with X0
S0 with X0  OS
0k0 = X0.
OS
0k0 = X0.
As HDRj(X
0/k0) is a finite dimensional k0 vector space, any
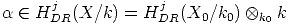
 k0
k0 (S), where k0
(S), where k0 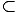
 (S)
(S) 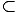 k and S is a smooth affine variety mapping to
S0. If x
k and S is a smooth affine variety mapping to
S0. If x 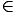 Ker
Ker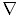 , then x lies in the kernel of
, then x lies in the kernel of
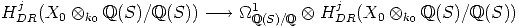
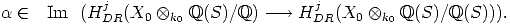
 S the smooth proper morphism obtained by base change
S
S the smooth proper morphism obtained by base change
S  S0 of f0. Making S smaller, one may assume that there is
S0 of f0. Making S smaller, one may assume that there is
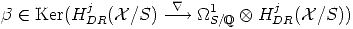
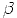
 OS
OS (S) =
(S) =  , and one wants to show that
, and one wants to show that 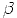
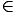 Im HDRj(X/
Im HDRj(X/ ).
).
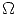 X/
X/ • one considers the filtration by the subcomplexes f*
• one considers the filtration by the subcomplexes f*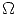 S/
S/ >a
>a 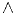
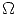 X/
X/ •-a. It defines a
spectral sequence
•-a. It defines a
spectral sequence
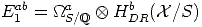
 ), whose d
1 differential is the Gauss-Manin connection
), whose d
1 differential is the Gauss-Manin connection 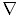 . As S is
affine, one has
. As S is
affine, one has
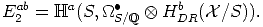


 )an, Xan = (X
)an, Xan = (X

 )an. The corresponding
spectral sequence
)an. The corresponding
spectral sequence
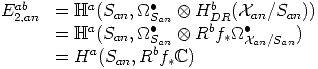
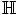 a+b(X
an,
a+b(X
an, 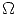 Xan•) = Ha+b(X
an,
Xan•) = Ha+b(X
an, ). This spectral sequence is, according to
Deligne ([11], (2.77) and (15.6)) the Leray spectral sequence, and by [2], (4.1.1) (i), it
degenerates at E2.
). This spectral sequence is, according to
Deligne ([11], (2.77) and (15.6)) the Leray spectral sequence, and by [2], (4.1.1) (i), it
degenerates at E2.
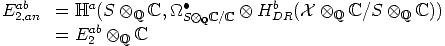


 degenerates at E2, and so does (E1ab,d
1). In particular
degenerates at E2, and so does (E1ab,d
1). In particular
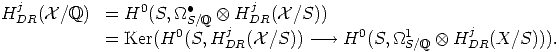
 (S).
(S).
Remark 5 In fact, even if S is not affine, there is a Leray spectral sequence for the de Rham cohomology [7] (3.3), which again degenerates at E2 by the comparison between the Leray spectral sequences for the Betti and the de Rham cohomologiesi, and the regularity of Gauss-Manin. For more on this, see [8].
Corollary 6 If  is an absolute Hodge cycle, then it is an absolute de Rham cycle.
is an absolute Hodge cycle, then it is an absolute de Rham cycle.
Proof. By [3] (2.5), we know that 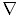
 = 0, where
= 0, where 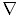 is as in (4) for j = 2i. Then we apply
(4).
is as in (4) for j = 2i. Then we apply
(4).
Corollary 7 If  is an absolute de Rham cycle such that I
is an absolute de Rham cycle such that I (
( )
) 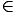 HB2i(X
HB2i(X
 ,
, ) for some
embedding
) for some
embedding 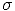 : k
: k 
 , then
, then  is an absolute Hodge cycle.
is an absolute Hodge cycle.
Proof. In fact, this is [3] (2.6). More precisely, choose S as in the proof of 4 and
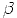
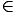 HDR2i(X/S) restricting to
HDR2i(X/S) restricting to  . The embeddings
. The embeddings  (S)
(S)  k
k  - -
- - 
 define a
define a  valued point of
S, which we still denote by
valued point of
S, which we still denote by 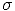 , such that
, such that 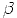 (
(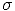 )
) 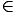 H2i((X
an)
H2i((X
an) ,
, )
) 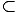 H2i((X
an)
H2i((X
an) ,
, ). The image
). The image
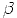 (
(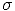 ) of
) of 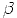 in
in
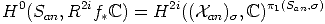
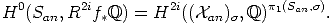
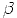 |(Xan)s is rational for all s, in particular for those s coming from an embedding
|(Xan)s is rational for all s, in particular for those s coming from an embedding
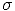 : k
: k 
 .
.
Remark 8 An advantage, if any, to adopt the language of absolute de Rham cycles consists of
dividing the question of wether  is absolute Hodge or not into two steps:
is absolute Hodge or not into two steps:
First of all  must be in
must be in
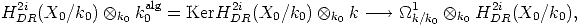
 must be in
must be in
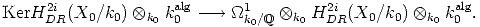
On the other hand, we have seen that if 
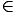 FiH
DR2i(X/k) is the class of an algebraic cycle,
then not only it is an absolute de Rham cycle, but also it is coming from
FiH
DR2i(X/k) is the class of an algebraic cycle,
then not only it is an absolute de Rham cycle, but also it is coming from 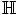 2i(X,
2i(X, 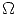 X/
X/ >i).
>i).
Let f : X  S,
S, 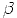
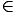 FiH
DRj(X/S) = H0(S,Rjf
*
FiH
DRj(X/S) = H0(S,Rjf
*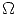 X/S>i), such that
X/S>i), such that 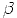

 (S)k =
(S)k = 
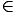 FiH
DRj(X/k)
as in the proof of 4. Let f
FiH
DRj(X/k)
as in the proof of 4. Let f : X
: X
 S
S be the smooth proper morphism obtained from f by
base change OS
be the smooth proper morphism obtained from f by
base change OS 

 , and
, and 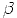
 be
be 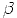


 . Let f
. Let f : X
: X
 S
S be a compactification of
f
be a compactification of
f such that
such that 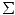 = S
= S - S
- S , D = f
, D = f -1(
-1(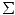 ) are normal crossing divisors and X
) are normal crossing divisors and X is
smooth.
is
smooth.
Definition 9 A class 
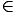 FiH
DRj(X/k) is said to be of moderate growth if for some (
FiH
DRj(X/k) is said to be of moderate growth if for some (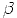 ,f
,f ) as
above, it verifies
) as
above, it verifies
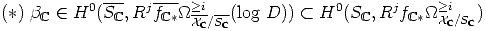
Remark 10 The definition 9 does not depend on the couple (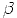 ,f
,f ) choosen. In fact, take (
) choosen. In fact, take (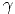 ,g)
with g : Y
,g)
with g : Y  T,
T,  (T)
(T) 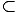 k, Y
k, Y
 (T)k = X,
(T)k = X, 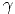

 (T)k =
(T)k =  . Then considering in k a function
field
. Then considering in k a function
field  (U) containing
(U) containing  (S) and
(S) and  (T), one has base changes
(T), one has base changes 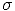 : U
: U  S,
S, 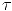 : U
: U  T,
fU : XU = X×SU
T,
fU : XU = X×SU  U, gU : YU = Y×T U
U, gU : YU = Y×T U  U, such that there is an isomorphism
U, such that there is an isomorphism
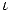 : XU
: XU  YU, with gU o
YU, with gU o 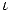 = fU,
= fU, 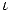 *(
*(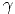
 OTOU) =
OTOU) = 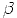
 OSOU, for U small enough. As
OSOU, for U small enough. As 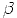
 fulfills
(*) on S
fulfills
(*) on S , it fulfills (*) on any blow up
, it fulfills (*) on any blow up 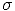
 : U
: U
 S
S such that a commutative diagram
exists
such that a commutative diagram
exists
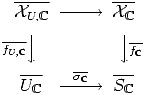
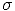
 -1
-1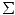 ,
,  = f
U,
= f
U, -1
-1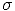
 -1
-1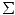 are normal crossing divisors, X
U,
are normal crossing divisors, X
U, and U
and U are smooth. Choose U
are smooth. Choose U such that
such that 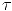 extends to
extends to 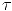
 : U
: U
 T
T , with a commutative
diagram
, with a commutative
diagram
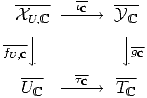
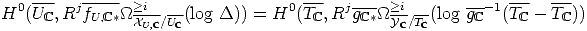
This implies in particular that classes of moderate growth build a k subvectorspace of FiH DRj(X/k).
Notation 11 We denote this subvectorspace by FiH
DRj(X,k)log, and by 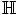 j(X,
j(X, 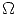 X/
X/ >i)log its
inverse image in
>i)log its
inverse image in 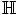 j(X,
j(X, 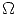 X/
X/ >i).
>i).
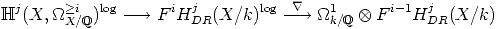
Proof. We have to prove that if 
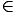 Ker
Ker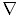 , then it lies in the image of
, then it lies in the image of 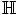 j(X,
j(X, 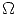 X/
X/ >i). With the
notations as above,
>i). With the
notations as above,
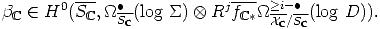
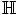 j(X
j(X ,
, 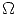 X
X
 /S
/S >i(log D)) and
defined as in [7] (3.3) on the complex
>i(log D)) and
defined as in [7] (3.3) on the complex  X
X /S
/S >i(log D). One has
>i(log D). One has
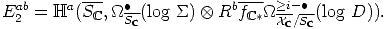
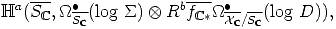
 *
* ) by [1] II, §6.
) by [1] II, §6.
Thus the spectral sequence degenerates at E2, and 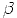
 comes from
comes from  j(X
j(X ,
, 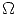 X
X
 >i(log D)). In
particular
>i(log D)). In
particular 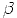
 comes from
comes from 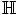 j(X,
j(X, 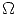 X/
X/ >i)
>i) 

 and the image of
and the image of  in
in
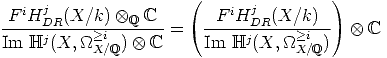
 lies in the image of
lies in the image of  j(X,
j(X,  X/
X/ >i).
>i).
Remark 13 If the transcendence degree of k is < 1, then of course the sequence
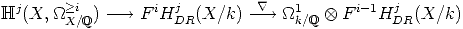
More generally, one can consider a k subvectorspace V of HDRj(X/k), such that I
 (V
(V 

 ) is
a Hodge substructure of HDRj(X
) is
a Hodge substructure of HDRj(X
 ,
, ). In the light of the above results, one can examine the
following questions.
). In the light of the above results, one can examine the
following questions.
Question 14 Is V stable under the Gauss-Manin connection?
For this, one would like I -1[I
-1[I
 (V
(V 

 )
) 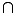 HBj(X
HBj(X
 ,
, )] to lie in V and to be independent of
)] to lie in V and to be independent of
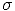 .
.
If so, then V defines a vector bundle W with a flat connection on S, where S is defined as in 4
such that V = W 
 (S)k, W
(S)k, W 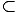 HDRj(X
0/k0)
HDRj(X
0/k0)  k0
k0 (S). Then Wan on San is generated by a
local system F.
(S). Then Wan on San is generated by a
local system F.
Question 15 In the above situation, is the monodromy representation associated to F defined
over  ?
?
Again, one can split up 14 into two parts as in 8. Moreover, the knowledge of 14 does not imply the knowledge of 15.
[1] Deligne, P.: Equations différentielles à points réguliers, Springer LN 169 (1970)
[2] Deligne, P.: Théorie de Hodge II, Publ. Math. de l’IHES 40 (1971), 5 - 58
[3] Deligne, P.: Hodge cycles on abelian varieties, in Hodge cycles, Motives and Shimura Varieties, Springer LN 900 (1982), 9 - 101
[4] Deligne, P.; Illusie, L.: Relèvements modulo p2 et décomposition du complexe de de Rham, Invent. math. 89 (1987), 247 - 270
[5] Grothendieck, A.: On the de Rham cohomology of algebraic varieties, Publ. Math. de l’IHES 29 (1966), 95 - 103
[6] Illusie, L.: Réduction semi-stable et décomposition de complexes de de Rham à coefficients, Duke Math. Journal 60, n01 (1990), 139 - 185
[7] Katz, N.: Nilpotent connections and the monodromy theorem: applications of a result of Turrittin, Publ. Math. de l’IHES 39 (1970), 175 - 232
[8] Paranjape, K.: Leray spectral sequence for de Rham cohomology, preprint
[9] Soulé, C.: Opérations en K-théorie algébrique, Canad. J. of Math. 37 n03 (1985), 488 - 550
[10] Srinivas, V.: Gysin maps and cycle classes for Hodge cohomology, preprint
[11] Zucker, S.: Hodge theory with degenerating coefficients: L2 cohomology in the Poincaré metric, Annals of Math. 109 (1979), 415 - 476