


Next: 1 Arithmetic of prime
Up: Introduction
Previous: Introduction
There are no solutions to the
following problem with (X, Y, Z) integers
| Xp + Yp + Zp |
= |
0 |
|
| XYZ |
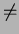 |
0 |
|
p 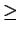 3 3 |
|
and a prime |
|
The approach to the proof of Fermat's Last Theorem that is
followed by A. Wiles in his recent attempt can be thought of as a
particular case of the following tactic.
Suppose (X, Y, Z) is a counter-example to Fermat's Last Theorem.
- To such a counter-example we attach a representation
Moreover, we have good ramification properties for this
representation. For example,
- the representation is unramified outside p,
- the representation has ``good'' ramification properties at
p.
- The next step is to use our knowledge of Algebraic Number Theory to
prove that such representations are impossible.
The proof of Kummer for the case of regular primes can also be
reviewed in this light. First of all, Kummer's proof associates to
every counter-example (X, Y, Z), a representation
where K is cyclotomic field of p-th roots of unity. Next, he
gives a way of finding out which primes p are such that we have such
a representation. As he showed, there are indeed such primes and thus
his proof works only for ``regular'' primes.
In section 1 we recall some computations in the cyclotomic
field of p-th roots of unity. In section 2 we show how a
counter-example to Fermat's Last Theorem (if it exists) can be used to
construct a cyclic extension of order p of the cyclotomic field
which is unramified everywhere. We review the Class number
formula in section 3. Finally, in Section 4 we use this formula
to check when such unramified extensions do indeed exist.
Most of the material in this note can be found in more detail
(though in a more classical presentation) in the book of H. M. Edwards
[1]. This re-examination of Kummer's proof was inspired
by some remarks made by V. Kumar Murty during his lecture on the
work of Wiles at the TIFR. I would like to thank A. Raghuram for his
careful reading of the manuscript and numerous suggestions.
We fix a prime p 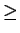 5 throughout the discussion.
5 throughout the discussion.



Next: 1 Arithmetic of prime
Up: Introduction
Previous: Introduction
Kapil Hari Paranjape
2002-11-22
5 throughout the discussion.