For any smooth projective variety we can form a countable collection
of projective schemes Hilbn (the Hilbert or Chow schemes) that
parametrise effective cycles of codimension p on X. Let C(X) be
a subgroup of ![]() (X). A homomorphism of groups from C(X) to the
group of rational points of a group variety A is called regular
if for any non-singular variety H parametrising cycles on X lying in
C(X), the resulting set maps from the set of rational points on H to the
set of rational points of A is induced by a morphism of varieties.
(X). A homomorphism of groups from C(X) to the
group of rational points of a group variety A is called regular
if for any non-singular variety H parametrising cycles on X lying in
C(X), the resulting set maps from the set of rational points on H to the
set of rational points of A is induced by a morphism of varieties.
In analogy with the picture for divisors one may ask the following questions:
There is no general geometric construction of the required Abelian variety. There is a complex torus associated to codimension p cycles, defined by Griffiths, which generalizes the Picard and Albanese varieties. This is called the pth intermediate Jacobian of X, and is defined by
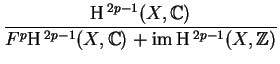 .
.
The Griffiths group
![]() (X) is
always countable, since all effective algebraic cycles of a fixed degree
are parametrized by the points of a (possibly reducible) Chow variety
of X; taking the union over all degrees, all effective algebraic
cycles lie in a countble collection of connected algebraic families, so
that
(X) is
always countable, since all effective algebraic cycles of a fixed degree
are parametrized by the points of a (possibly reducible) Chow variety
of X; taking the union over all degrees, all effective algebraic
cycles lie in a countble collection of connected algebraic families, so
that
![]() (X)/
(X)/![]() (X) is countable. Hence if
(X) is countable. Hence if
![]() (X)
(X) ![]() 0 for some i > p, then the Abel-Jacobi map cannot be surjective. The
restriction of the Abel-Jacobi map to
0 for some i > p, then the Abel-Jacobi map cannot be surjective. The
restriction of the Abel-Jacobi map to
![]() (X) is a regular
homomorphism onto the Abelian variety which is its image; conjecturally,
this is the universal regular homomorphism, as in the case of the Albanese
map. One also expects the Abel-Jacobi map to be injective on torsion, in
general. The injectivity of the Abel-Jacobi map on torsion is known for
codimension 2 cycles, from work of Merkurjev and Suslin on the K-theory of
division algebras, combined with results of Bloch and Ogus; we discuss
this below. The universality of the Abel-Jacobi map on
(X) is a regular
homomorphism onto the Abelian variety which is its image; conjecturally,
this is the universal regular homomorphism, as in the case of the Albanese
map. One also expects the Abel-Jacobi map to be injective on torsion, in
general. The injectivity of the Abel-Jacobi map on torsion is known for
codimension 2 cycles, from work of Merkurjev and Suslin on the K-theory of
division algebras, combined with results of Bloch and Ogus; we discuss
this below. The universality of the Abel-Jacobi map on
![]() (X) has
been proved by Murre [27] using the injectivity on torsion.
(X) has
been proved by Murre [27] using the injectivity on torsion.