


Next: Functions, continuity and differentiability
Up: Pre-requisites
Previous: Polynomials in more than
In this section we revise the notion of convergence for real numbers
and prove the Bolzano-Weierstrass property.
From section 1 we have a least upper bound (greatest lower bound) for
any bounded increasing (respectively decreasing) sequence of real
numbers.
Exercise 28
Show that any bounded non-decreasing sequence of real numbers has a
least upper bound; a bounded non-increasing sequence has a greatest
lower bound.
Now if S is any bounded non-empty set of real numbers, let c1 be an
upper bound and s1 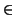 S. Now we iteratively define a pair of
sequences {sn} and {cn} as follows. If
(sn + cn)/2 is an
upper bound for S then we define
sn + 1 = sn and
cn + 1 = (sn + cn)/2; otherwise let sn + 1 be any element of S
so that
sn + 1 > (sn + cn)/2 and
cn + 1 = cn.
S. Now we iteratively define a pair of
sequences {sn} and {cn} as follows. If
(sn + cn)/2 is an
upper bound for S then we define
sn + 1 = sn and
cn + 1 = (sn + cn)/2; otherwise let sn + 1 be any element of S
so that
sn + 1 > (sn + cn)/2 and
cn + 1 = cn.
Exercise 29
Show that {
sn} is a non-decreasing sequence of elements of
S
and {
cn} is a non-increasing sequence of upper bounds for
S
so that
(
cn + 1 -
sn + 1)
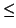
(
sn -
cn)/2. Hence show that the
greatest lower bound of {
cn} is equal to the least upper bound
of {
sn} and this bound is the least upper bound for
S.
In particular, if {xn} is any bounded sequence of real numbers we
have a least upper bound and greatest lower bound for this sequence.
Let us define
| lk |
= |
the greatest lower bound of {xn| n 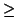 k} k} |
|
| uk |
= |
the least upper bound of {xn| n 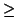 k} k} |
|
| liminf{xn} |
= |
the least upper bound of {lk} |
|
| limsup{xn} |
= |
the greatest lower bound of {uk} |
|
Note that {lk} is a non-decreasing sequence and {uk} is a
non-increasing sequence.
Exercise 30
Show that
liminf{
xn}
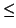
limsup{
xn}.
We say that the sequence {xn} has a limit (is convergent) if
these two numbers are equal; this number c is called the limit
of this sequence of numbers.
Exercise 31
Show that for every positive
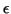
there is a index
n0 so
that
|
xn -
c| <
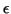
for all
n >
n0. Hence, there is an
index
n1 so that
|
xn -
xm| <
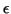
for all
n >
n1; this
called Cauchy's criterion. Conversely show that any
sequence {
xn} that satisfies Cauchy's criterion is convergent.
Now for any sequence {xn} we can find subsequences
{yk = xnk} (with
n1 < n2 < ... ) so that {yk} is
convergent (this is called the Bolzano-Weierstrass property).
Exercise 32
Show that there are subsequences of {xn} that converge to
liminf{xn} and
limsup{xn}.
Finally, let us note some algebraic properties of convergent
sequences.
Exercise 33
Show that the sum, difference and product of convergent sequences is
limit of the sum, difference and product of the terms. If a sequence
has a non-zero limit then show that the inverse of the limit is the
limit of the inverses of the non-zero terms of the sequence.



Next: Functions, continuity and differentiability
Up: Pre-requisites
Previous: Polynomials in more than
Kapil H. Paranjape
2001-01-20