Putting co-ordinates

First of all we expand our geometry and introduce ideal points, lines and planes. This can be considered as the process of re-constructing P³(K) given [R].

The definition of an ideal point (Point) is motivated by the fact that a pair of intersecting lines is lies in a plane.

Definition 4   A Point is a collection of lines so that any pair of lines in this collection is co-planar. Moreover, there is at least one line in this collection through any given point.

The relation of these properties to Desargues' theorem is given by.

Theorem 10   Let a, b, c be any three lines in the collection of lines determining a Point. There are points A, A' on a, B, B' on b and C, C' on c which give a Desarguian configuration. That is to say, the lines AB and A'B' intersect in a point C'', the lines AC and A'C' intersect in a point B'' and the lines CB and C'B' intersect in a point A'', so that the point A'', B'' and C'' lie on a line.

Similar ideas can be used to show that there are Points.

Exercise 9   Let l and m be lines and consider the collection of all lines k such that either one of the following holds:

1. k is not co-planar with l and m but is co-planar with each of l and m separately.
2. There is a line j of the above type so that j is co-planar with each of k, l, m.

Check that this collection gives a Point.

The notion of collinearity for Points can be defined as follows

Definition 5   The Points A, B and C is said to be collinear if for any point p there are lines a, b and c in the collections A, B and C respectively so that a, b and c are coplanar.

With this definition we can define an ideal line

Definition 6   A Line is a collection of Points so that any three are collinear; moreover, the collection contains at least two Points.

We easily check

Exercise 10   There is a unique Line containing a pair of Points.

Similarly, we can define an ideal plane

Definition 7   A Plane is a collection of Points and Lines so that there is at least one Point and one Line not containing it in the collection. If a Line is in the collection then so is every Point contained in the Line. If a Line and a Point not on it are contained in the collection so is every Line containing the Point and a Point of the Line. Finally, there is at least one Point not in the collection.

The main result is then

Theorem 11   If we start with a geometry satisfying the axioms of incidence and order, then the Points, Lines and Planes as defined above satisfy the axioms of incidence and the projective axiom of parallels.

Since each point, line and plane in the original geometry determines a Point, Line and Plane respectively, we see that we have ``embedded'' our geometry in a geometry satisfying the axioms of incidence and the projective axiom of parallels. Such a geometry is called an axiomatic projective geometry. By replacing the use of Pasch axiom by the use of the projective axiom of parallels one can also prove Desargues' theorem for this geometry. We wish to co-ordinatise this geometry.

The addition and multiplication operations can be ``constructed'' in a manner similar to that in Euclidean geometry.

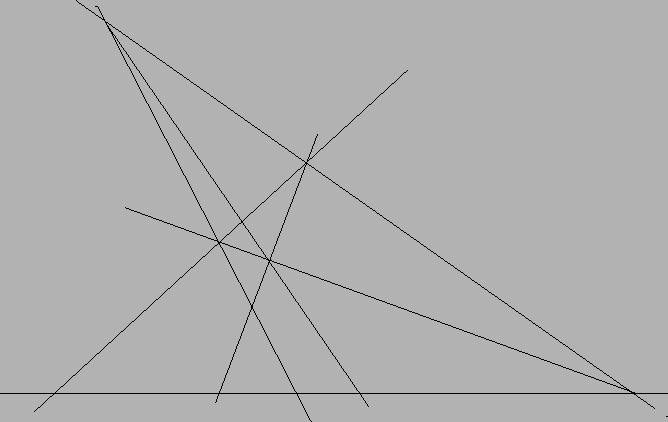
Definition 8   Let O and Z be a pair of Points and A, B be Points on the Line j containing O and Z. Let k be any Line containing Z and not O and P be a point of k other than Z. Let Q be a Point on the Line l joining O and P other than these two. The Line m joining Z and Q meets the Line n joining A and P in a Point C. Let D be the Point of intersection of the Line o joining B and Q. Finally E is the Point of intersection of the line p joining C and D with the line j. We then say that E is the ``sum'' of the points A and B with respect to O and Z.

picture(6999,4422)(2209,-4468) (2731,-4426)(0,0)[lb]O (4411,-4396)(0,0)[lb]A (5236,-4366)(0,0)[lb]B (8821,-4351)(0,0)[lb]Z (4201,-2701)(0,0)[lb]P (5281,-1606)(0,0)[lb]Q (5131,-2791)(0,0)[lb]C (3346,-181)(0,0)[lb]D (5971,-4441)(0,0)[lb]E
The sum of A and B with respect to O and Z is E.

Exercise 11   Show that this operation is well-defined.

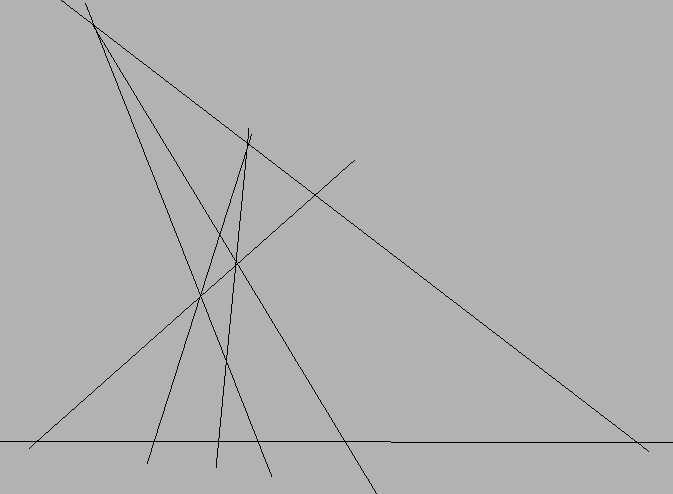
Definition 9   Let O, I and Z be distinct collinear Points and A, B be Points on the Line j containing O and Z. Let C be a Point not on j. Let k be the Line joining C with Z and l be the Line joining C with O. Let J be a Point on l different from C and O. The Line m joining I and J meets l in a point K. Let C be the Point of intersection of the Line n joining A and K. Let D be the Point of intersection of the Line joining B and J. Finally, let E be the Point on j that lies on the line o that joins C and D. We say that E us the ``product'' of the points A and B with respect to O, I and Z.

picture(7044,5184)(2254,-4963) (2506,-4696)(0,0)[lb]O (3766,-4696)(0,0)[lb]I (4471,-4681)(0,0)[lb]A (4966,-4651)(0,0)[lb]B (8806,-4651)(0,0)[lb]Z (4156,-2926)(0,0)[lb]J (5596,-1681)(0,0)[lb]K (4786,-1111)(0,0)[lb]L (4831,-2371)(0,0)[lb]C (3346, -1)(0,0)[lb]D (5776,-4711)(0,0)[lb]E
The product of A and B with respect to O, I and Z is E.

Exercise 12   Show that this operation is well-defined.

The main result is to use these operations to show that

Theorem 12   Let O, I and Z be distinct Points on a Line j. The operations defined above make the collection of all Points on j other than Z into a (skew-) field K.

Finally, one produces a one-to-one correspondence

Theorem 13   There is a one-to-one correspondence between the (axiomatic) projective geometry and the geometry P³(K).

The original geometry is then that of a convex set R in A³(K).