In spite of the axioms of order being ignored for so many hundreds of
years they are so important that one can entirely replace the axioms
of incidence by giving an extended set of axioms of order. Think of it
this way. If a straight line is to be the shortest path from a point
to another then we must at least be able to say what are the points
``on the way'' or in-between.
The following theorems can be deduced from the axioms of Incidence and
Order.
Proof.
In case the plane
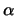
containing the points
A,
B and
C does not
contain all of the points
A',
B' and
C' then the line containing
the points
A'',
B'' and
C'' is just the line of intersection of
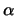
with the plane
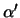
determined by
A',
B' and
C'. Thus, the theorem needs only to be proved under the assumption
that all the points lie in a plane. In this case we shall show how to
construct
A''',
B''' and
C''' that do not lie in the plane and
so that the points
A,
B,
C,
A''',
B''' and
C''' also
satisfy the hypothesis of the theorem. Moreover,
A''',
B''' and
C'' are collinear and so on cyclically. Thus, the planar version
will then follow from the non-planar version.
picture(8379,7452)(949,-6688)
(4366,-3556)(0,0)[lb]A
(4201,-6571)(0,0)[lb]A'
(3076,-4066)(0,0)[lb]B'
(3526,-2716)(0,0)[lb]B
(5581,-3136)(0,0)[lb]C
(5716,-3826)(0,0)[lb]C'
(6331,-2326)(0,0)[lb]B''
(2041,-826)(0,0)[lb]C''
(8251,-3076)(0,0)[lb]A''
(4936,629)(0,0)[lb]O
The triangles ABC and A'B'C' lie in different planes.
In the remaining cases we examine all the possibilities for
between-ness for the triples (
A,
A',
O), (
B,
B',
O) and (
C,
C',
O). By
interchanging the
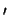
and permuting the letters (
A,
B,
C) we
can reduce to the following two cases.
- A does not lie between A' and O, B does not lie between
B' and O, C does not lie between C' and O.
- A' lies between A and O, B' does not lie between
B and O, C' does not lie between C and O.
picture(9549,6694)(139,-7790)
(601,-2611)(0,0)[lb]A''
(1201,-7336)(0,0)[lb]A
(2551,-5236)(0,0)[lb]B
(5026,-7261)(0,0)[lb]C
(7501,-4186)(0,0)[lb]O
(4351,-6211)(0,0)[lb]A'
(3751,-5236)(0,0)[lb]B'
(5776,-6436)(0,0)[lb]C'
(5251,-3211)(0,0)[lb]A'''
(4501,-3436)(0,0)[lb]B'''
(3526,-3811)(0,0)[lb]C''
(5926,-3736)(0,0)[lb]C'''
(9151,-6211)(0,0)[lb]B''
(6076,-2011)(0,0)[lb]O''
(5476,-1261)(0,0)[lb]O'
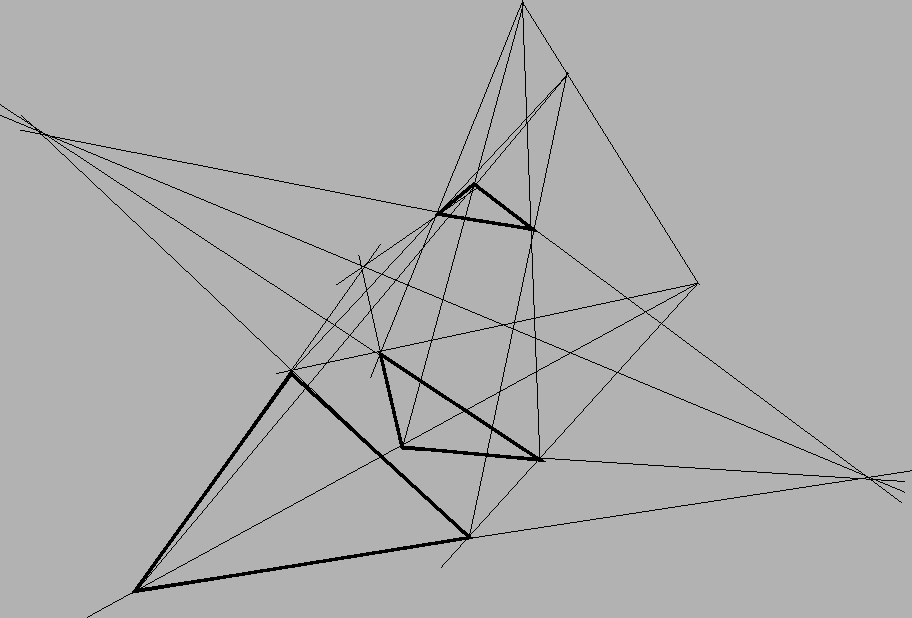
Lifting A'B'C' in the first case.
Examining the first case, let
O' be a point not in the plane of
A,
B and
C. Let
A''' be a point between
A' and
O'. The line
joining
A and
A''' then must contain a point
O'' lying between
O and
O' since its intersection with the line joining
A' and
O
is
A which does not lie between these points by hypothesis. Now the
line joining
O'' and
B contains a point
O'' between
O and
O'
and thus must contain a point
B''' between
O' and
B' since the
point
B of intersection of this line with the line joining
B' and
O is not between these two points. Similarly, we obtain
C''' lying
on the line joining
C and
O'' and lying between
O' and
C'.
picture(5850,7924)(1351,-8461)
(4651,-8461)(0,0)[lb]B
(7201,-5761)(0,0)[lb]C'
(5326,-3661)(0,0)[lb]B'
(5476,-4786)(0,0)[lb]O
(3526,-6436)(0,0)[lb]A'
(1426,-961)(0,0)[lb]A'''
(3226,-5011)(0,0)[lb]O'
(4276,-4036)(0,0)[lb]C
(4051,-1936)(0,0)[lb]A''
(2551,-4786)(0,0)[lb]C'''
(2776,-6436)(0,0)[lb]B''
(1651,-5761)(0,0)[lb]B'''
(1351,-5311)(0,0)[lb]O''
(1531,-7636)(0,0)[lb]A
(2341,-7786)(0,0)[lb]C''
Lifting A'B'C' in the second case.
In the second case we choose a point
O'' which does not line in the
plane of
A,
B and
C. Let
A''' be a point so that
O'' lies
between
A and
A'''. Now the line joining
A' and
A''' contains
the point
A' which lies between
A and
O; moreover its intersection
with the line joining
A and
O'' is
A''' which does not lie
between these points. Thus the there is a point
O' on the line
joining
A' and
A''' which lies between
O'' and
O'. Now,
consider the line joining
O' and
B' and the triangle of points
O'',
B and
O. As before we find a point
B''' which lies between
B and
O'' and on the line joining
O' and
B'. Similarly, we
find
C'''.
In both these cases the line joining A''' and B''' meets the plane
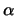 within the intersection of the plane determined by A', B'
and O' and the plane
within the intersection of the plane determined by A', B'
and O' and the plane 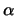 ; this is the line joining A' and
B'. Similarly, the intersection of the line joining A''' and
B''' with
; this is the line joining A' and
B'. Similarly, the intersection of the line joining A''' and
B''' with 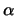 lies within the intersection of the plane
determined by A, B and O'' with the plane
lies within the intersection of the plane
determined by A, B and O'' with the plane 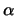 ; this is the
line joining A and B. In other words, the line joining A''' and
B''' contains the point C''. We prove the other containments
cyclically.
; this is the
line joining A and B. In other words, the line joining A''' and
B''' contains the point C''. We prove the other containments
cyclically.



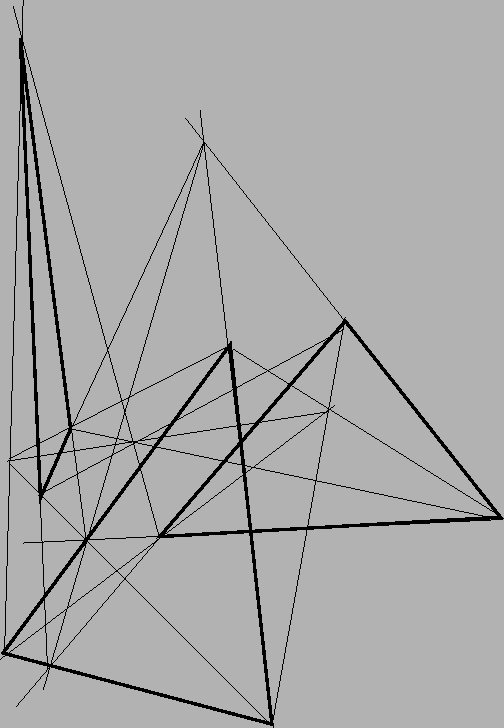
![]() within the intersection of the plane determined by A', B'
and O' and the plane
within the intersection of the plane determined by A', B'
and O' and the plane ![]() ; this is the line joining A' and
B'. Similarly, the intersection of the line joining A''' and
B''' with
; this is the line joining A' and
B'. Similarly, the intersection of the line joining A''' and
B''' with ![]() lies within the intersection of the plane
determined by A, B and O'' with the plane
lies within the intersection of the plane
determined by A, B and O'' with the plane ![]() ; this is the
line joining A and B. In other words, the line joining A''' and
B''' contains the point C''. We prove the other containments
cyclically.
; this is the
line joining A and B. In other words, the line joining A''' and
B''' contains the point C''. We prove the other containments
cyclically.
![]()
