MORPHISMS
KAPIL HARI PARANJAPE
1. Morphisms
When we defined affine schemes as functors on the category of Finite rings we were a bit
vague on what exactly morphisms were. In the case of projective schemes we didn’t
even try to define the notion. A morphism of schemes f : X  Y is a natural
transformation of functors such that the graph is a closed subscheme. Recall that a
natural transformation of functors on the category of finite rings gives a map
f(A) : X(A)
Y is a natural
transformation of functors such that the graph is a closed subscheme. Recall that a
natural transformation of functors on the category of finite rings gives a map
f(A) : X(A)  Y (A) for every finite ring A and for every morphism A
Y (A) for every finite ring A and for every morphism A  B the
following diagram commutes.
B the
following diagram commutes.
The product X ×Y has been given a natural structure of a scheme. The graph  f(A) is a
sub-functor of X(A) × Y (A) = (X × Y )(A) and so it makes sense to require
that there is a closed subscheme Z of X × Y such that Z(A) =
f(A) is a
sub-functor of X(A) × Y (A) = (X × Y )(A) and so it makes sense to require
that there is a closed subscheme Z of X × Y such that Z(A) =  f(A) for all
A.
f(A) for all
A.
We note that for any pair of rings R and S, the product Spec(R) × Spec(S) is just
Spec(R  S). We have so far been using ring homomorphisms R
S). We have so far been using ring homomorphisms R  S to obtain
morphisms Spec(S)
S to obtain
morphisms Spec(S)  Spec(R); it is clear that this gives a natural transformation of
functors.. Note that such a ring homomorphism gives a surjective homomorphism
R
Spec(R); it is clear that this gives a natural transformation of
functors.. Note that such a ring homomorphism gives a surjective homomorphism
R  S
S  S by “multiplication”. This gives Spec(S) as a closed sub-scheme of
Spec(R) × Spec(S) and this closed sub-scheme is the graph of the above natural
transformation.
S by “multiplication”. This gives Spec(S) as a closed sub-scheme of
Spec(R) × Spec(S) and this closed sub-scheme is the graph of the above natural
transformation.
We will now prove the converse. First of all, exactly as above, we note that what is
required in oder to obtain a morphism is a closed subscheme Z of Spec(R) × Spec(S)
such that Z(A)  Spec(S)(A) is a bijection for all finite rings A (the graph of a map of
sets projects bijectively onto the the domain of the map). Thus we will conclude our
proof if we can show that any such map is an isomorphism. Since Z is itself the closed
sub-scheme of an affine scheme it too is Spec(S') for some ring S; moreover,
we have a natural homomorphism S
Spec(S)(A) is a bijection for all finite rings A (the graph of a map of
sets projects bijectively onto the the domain of the map). Thus we will conclude our
proof if we can show that any such map is an isomorphism. Since Z is itself the closed
sub-scheme of an affine scheme it too is Spec(S') for some ring S; moreover,
we have a natural homomorphism S  R
R  S that induces the projection.
Hence we have reduced our problem to the following statement. Let S
S that induces the projection.
Hence we have reduced our problem to the following statement. Let S  S' be
a homomorphism of finitely generated rings such that for every finite ring A
the resulting map Hom(S',A)
S' be
a homomorphism of finitely generated rings such that for every finite ring A
the resulting map Hom(S',A)  Hom(S,A) is a bijection, then S
Hom(S,A) is a bijection, then S  S' is an
isomorphism.
S' is an
isomorphism.
The proof of this statement will be in many parts. First of all we will prove a
condition for finite-ness. We will use this to show that S  S' is finite. An application
of Nakayama’s lemma and another finite-ness theorem will then conclude the
result.
S' is finite. An application
of Nakayama’s lemma and another finite-ness theorem will then conclude the
result.
1.1. Finite-ness. Let f : R  S be a homomorphism of rings such that the induced
homomorphism f : R[X]
S be a homomorphism of rings such that the induced
homomorphism f : R[X]  S[X] is closed. Recall that this means that for any ideal I in
S[X], and any maximal ideal M in R[X] containing f-1(I), there is a maximal ideal N
in S[X] such that f(M)
S[X] is closed. Recall that this means that for any ideal I in
S[X], and any maximal ideal M in R[X] containing f-1(I), there is a maximal ideal N
in S[X] such that f(M)  N. We claim that this condition implies that R
N. We claim that this condition implies that R  S is
finite.
It is enough to show that any element a in S satisfies a monic polynomial
with coefficients in R. Consider the ideal (1 - aX) in S[X]; if P(X) lies in
f-1((1 - aX)), and Q(X) = Xdeg(P)P(X-1) then P(a) = 0. So we need to show that
f-1((1 - aX)) contains a monic polynomial. Let J be the ideal in R generated by the
leading coefficient of elements of f-1((1 - aX)). This ideal is the image in
R of the ideal f-1((1 - aX)) under the map R[X]
S is
finite.
It is enough to show that any element a in S satisfies a monic polynomial
with coefficients in R. Consider the ideal (1 - aX) in S[X]; if P(X) lies in
f-1((1 - aX)), and Q(X) = Xdeg(P)P(X-1) then P(a) = 0. So we need to show that
f-1((1 - aX)) contains a monic polynomial. Let J be the ideal in R generated by the
leading coefficient of elements of f-1((1 - aX)). This ideal is the image in
R of the ideal f-1((1 - aX)) under the map R[X]  R that sends X to 0.
Now, if J is not the unit ideal then its inverse image f-1((1 - aX)) + (X)
must be contained in a maximal ideal M of R[X]. By the closed-ness, there is a
maximal ideal N of S[X] that lies over it and contains ((1 - aX)). But then N
contains 1 - aX and X as well; a contradition. Thus J must be the unit ideal as
required.
R that sends X to 0.
Now, if J is not the unit ideal then its inverse image f-1((1 - aX)) + (X)
must be contained in a maximal ideal M of R[X]. By the closed-ness, there is a
maximal ideal N of S[X] that lies over it and contains ((1 - aX)). But then N
contains 1 - aX and X as well; a contradition. Thus J must be the unit ideal as
required.
1.2. Finite rings. Let R  S be a morphism of finitely generated rings with
Hom(S,A)
S be a morphism of finitely generated rings with
Hom(S,A)  Hom(R,A) a bijection for all finite rings A. We now prove the result in
case one of the rings is finite.
Now if R is finite then we can take A = R and obtain a bijection Hom(S,R)
Hom(R,A) a bijection for all finite rings A. We now prove the result in
case one of the rings is finite.
Now if R is finite then we can take A = R and obtain a bijection Hom(S,R)  Hom(R,R).
In particular, we obtain a homomorphism S
Hom(R,R).
In particular, we obtain a homomorphism S  R such that the composite
R
R such that the composite
R  S
S  R is identity on R. Consider the homomorphism S
R is identity on R. Consider the homomorphism S  R and the
induced map Hom(R,A)
R and the
induced map Hom(R,A)  Hom(S,A). By composing this with the bijection
Hom(S,A)
Hom(S,A). By composing this with the bijection
Hom(S,A)  Hom(R,A) we obtain the identity map Hom(R,A)
Hom(R,A) we obtain the identity map Hom(R,A)  Hom(R,A). It
follows that Hom(R,A)
Hom(R,A). It
follows that Hom(R,A)  Hom(S,A) is a bijection as well. Thus if S is finite as well, we
see that R
Hom(S,A) is a bijection as well. Thus if S is finite as well, we
see that R  S is an isomorphism as required.
S is an isomorphism as required.
So we can assume that we are in the situation of the theorem where in addition S is
finite but we are not sure if R is. Let M be any maximal ideal of R of S. As proved in
the previous section R/M is finite and so taking A = R/M we have a natural
homomorphism R  A = R/M. By assumption this factors as R
A = R/M. By assumption this factors as R  S
S  A, so f(M) is
contained in the kernel of S
A, so f(M) is
contained in the kernel of S  A which is a maximal ideal N of S. Thus every maximal
ideal in R is of the form f-1(N) for some maximal ideal N of S. Since S is finite
it has only finitely many maximal ideals; thus R too has only finitely many
maximal ideals. As we have seen in the previous section this means that R is
finite.
A which is a maximal ideal N of S. Thus every maximal
ideal in R is of the form f-1(N) for some maximal ideal N of S. Since S is finite
it has only finitely many maximal ideals; thus R too has only finitely many
maximal ideals. As we have seen in the previous section this means that R is
finite.
1.3. Co-finite ideals. Let R  S be as before. Let I be an ideal of R. We obtain a
homomorphism R/I
S be as before. Let I be an ideal of R. We obtain a
homomorphism R/I  S/f(I)S; consider the map Hom(S/f(I)S,A)
S/f(I)S; consider the map Hom(S/f(I)S,A)  Hom(R/I,A).
The former term is contained in Hom(S,A) and the latter in Hom(R,A) thus the map is
injective. On the other hand a homomorphism R/I
Hom(R/I,A).
The former term is contained in Hom(S,A) and the latter in Hom(R,A) thus the map is
injective. On the other hand a homomorphism R/I  A is the same as a homomorphism
R
A is the same as a homomorphism
R  A which is zero on I. By assumption, this factors as a homomorphism
R
A which is zero on I. By assumption, this factors as a homomorphism
R  S
S  A which means that the homomorphism S
A which means that the homomorphism S  A is 0 on f(I). Thus
Hom(S/f(I)S,A)
A is 0 on f(I). Thus
Hom(S/f(I)S,A)  Hom(R/I,A) is a bijection.
In particular, if I is such that R/I is finite, we see that R/I
Hom(R/I,A) is a bijection.
In particular, if I is such that R/I is finite, we see that R/I  S/f(I)S is an
isomorphism.
S/f(I)S is an
isomorphism.
Now suppose that J is an ideal of S such that S/J is finite and put I = f-1(J) so
that R/I  S/J is injective. Then R/I is finite and so R/I
S/J is injective. Then R/I is finite and so R/I  S/f(I)S is an
isomorphism. But J contains f(I)S and the intersection of J/f(I)S with R/I is 0. Thus
J = f(I)S.
S/f(I)S is an
isomorphism. But J contains f(I)S and the intersection of J/f(I)S with R/I is 0. Thus
J = f(I)S.
What we have proved is that the maps J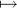 fJ and I
fJ and I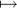 f(I)S induce a bijection
between co-finite ideals in R and S. Moreover, we have R/I
f(I)S induce a bijection
between co-finite ideals in R and S. Moreover, we have R/I  S/J is an isomorphism in
this situation.
S/J is an isomorphism in
this situation.
1.4. Relative Noether Normalisation. Let R be a finitely generated domain and
f : R  S be any injective morphism with S finitely generated as an R-algebra.
Let X1, X2. ..., Xn be a maximal subset (of some fixed set of generators)
of S that is transcendental over the quotient field of R. We have an injective
morphism R1 = R[X1,...,Xn]
S be any injective morphism with S finitely generated as an R-algebra.
Let X1, X2. ..., Xn be a maximal subset (of some fixed set of generators)
of S that is transcendental over the quotient field of R. We have an injective
morphism R1 = R[X1,...,Xn]  S and for any generator g of S, there is a
polynomial P(T)
S and for any generator g of S, there is a
polynomial P(T) 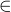 R1[T] and a
R1[T] and a 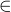 R1 with a
R1 with a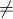 0 such that P(ag) = 0. Collecting
denominators, there is a non-zero element d in R1 such that (R1)d
0 such that P(ag) = 0. Collecting
denominators, there is a non-zero element d in R1 such that (R1)d  Sd is finite and
injective.
Let d0 be any coefficient of d that is non-zero. As R is a finitely generated domain
there is a maximal ideal M that does not contain d0. Now M[X1,...,Xn] is a prime ideal
P in R1 that d does not lie in. Hence it gives a prime ideal in (R1)d. Since (R1)d
Sd is finite and
injective.
Let d0 be any coefficient of d that is non-zero. As R is a finitely generated domain
there is a maximal ideal M that does not contain d0. Now M[X1,...,Xn] is a prime ideal
P in R1 that d does not lie in. Hence it gives a prime ideal in (R1)d. Since (R1)d  Sd is
finite and injective we have PSd
Sd is
finite and injective we have PSd 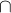 (R1)d = Pd. It follows that, if K denotes R/M,
K[X1,...,Xn]d
(R1)d = Pd. It follows that, if K denotes R/M,
K[X1,...,Xn]d  (Sd)/(PSd) is finite and injective. If n > 0 then this would mean that
there are infinitely many maximal ideals is Sd (and hence in S) that lie over
M.
(Sd)/(PSd) is finite and injective. If n > 0 then this would mean that
there are infinitely many maximal ideals is Sd (and hence in S) that lie over
M.
If particular, applying this in our situation R  S as above, we see that n = 0;
equivalently R1 = R. In other words, if R is a domain and f : R
S as above, we see that n = 0;
equivalently R1 = R. In other words, if R is a domain and f : R  S is an injective
homomorphism that induces a bijection between co-finite ideals in R and S then there is
a non-zero element d in R so that Rd
S is an injective
homomorphism that induces a bijection between co-finite ideals in R and S then there is
a non-zero element d in R so that Rd  Sd is finite.
Sd is finite.
If Q' is any prime such that Q'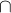 R = (0), the element d does not lie in Q' so that Q'd
is a prime in Sd. Since Rd
R = (0), the element d does not lie in Q' so that Q'd
is a prime in Sd. Since Rd  Sd is finite it follows that Q'd is minimal in Sd; hence Q' is
minimal in S as well.
Sd is finite it follows that Q'd is minimal in Sd; hence Q' is
minimal in S as well.
Suppose that Q and Q' are two distinct minimal primes in Sd. Let a be an element of
Q' that is not in Q and consider a maximal ideal N in Sd whose image in Sad is a
non-trivial maximal ideal containing the Qad. Let M = N 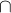 R; by the going up theorem
we can find a maximal ideal N' in Sd that contains Q'. Since a lies in N' and not in N,
these are distinct maximal ideals in Sd over M. This contradicts the bijection between
co-finite ideals in R and S.
R; by the going up theorem
we can find a maximal ideal N' in Sd that contains Q'. Since a lies in N' and not in N,
these are distinct maximal ideals in Sd over M. This contradicts the bijection between
co-finite ideals in R and S.
The minimal prime Q in S such that Q 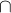 R = (0) is thus unique. We now want to
show that there are no minimal primes of the other type either.
R = (0) is thus unique. We now want to
show that there are no minimal primes of the other type either.
1.5. Krull’s Intersection Theorem. Let M be any maximal ideal in a finitely
generated ring R. Consider the graded ring 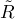 = R
= R 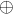 M
M 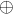 M2
M2 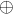
 . Let I =
. Let I =  Mn; then
Mn; then
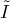 = I
= I  I
I 
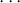 is a graded ideal in
is a graded ideal in 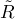 . In particular, it is finitely generated. Let x1, ...,
xn be a homogeneous system of generators and d be larger than all their degrees.
Expressing elements of degree d in
. In particular, it is finitely generated. Let x1, ...,
xn be a homogeneous system of generators and d be larger than all their degrees.
Expressing elements of degree d in 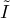 in terms of the generators, we conclude that
I = MI. By Nakayama’s lemma we get I = 0.
Let f : R
in terms of the generators, we conclude that
I = MI. By Nakayama’s lemma we get I = 0.
Let f : R  S be a homomorphism of finitely generated rings which induces a
bijection between co-finite ideals such that R/I
S be a homomorphism of finitely generated rings which induces a
bijection between co-finite ideals such that R/I  S/f(I)S is an isomorphism for every
co-finite ideal I. Let M be any maximal ideal in R and N = f(M)S be the corresponding
maximal ideal in S. We have an isomorphism R/Mk
S/f(I)S is an isomorphism for every
co-finite ideal I. Let M be any maximal ideal in R and N = f(M)S be the corresponding
maximal ideal in S. We have an isomorphism R/Mk  S/Nk for all k. Applying the
intersection theorem we conclude that ker(f) = (0).
S/Nk for all k. Applying the
intersection theorem we conclude that ker(f) = (0).
Now let us assume in addition that R is a domain. If possible, let Q be a minimal
prime in S such that Q 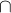 R
R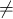 (0). Let a be an element of the product of the remaining
minimal primes that is not in Q. Then Qa is the unique minimal prime in Sa so
it consists of nilpotent elements. Since R is a domain, we see that R
(0). Let a be an element of the product of the remaining
minimal primes that is not in Q. Then Qa is the unique minimal prime in Sa so
it consists of nilpotent elements. Since R is a domain, we see that R  Sa
has a non-trivial kernel. Let N be a maximal ideal of S not containing a and
M = f-1(N). Then (Sa)/(NkSa) = S/Nk for all k so that R/MK
Sa
has a non-trivial kernel. Let N be a maximal ideal of S not containing a and
M = f-1(N). Then (Sa)/(NkSa) = S/Nk for all k so that R/MK  (Sa)/(NkSa)
is an isomorphism for all k. But this contradicts the existence of a kernel for
R
(Sa)/(NkSa)
is an isomorphism for all k. But this contradicts the existence of a kernel for
R  Sa.
Sa.
1.6. Closed-ness. Let R  S be a morphism of finitely generated rings that
induces a bijection between co-finite ideals as above. Let Q be a prime ideal in
S and P = f-1(Q). We can consider the map R/P
S be a morphism of finitely generated rings that
induces a bijection between co-finite ideals as above. Let Q be a prime ideal in
S and P = f-1(Q). We can consider the map R/P  S/f(P)S which has
the same properties as R
S/f(P)S which has
the same properties as R  S; in addition R/P is a domain and the map is
injective. Replacing R by R/P and S by S/f(P)S we see that we have an injective
homomorphism R
S; in addition R/P is a domain and the map is
injective. Replacing R by R/P and S by S/f(P)S we see that we have an injective
homomorphism R  S that induces a bijection between co-finite ideals and R is a
domain. Moreover, Q is a prime ideal in S such that Q
S that induces a bijection between co-finite ideals and R is a
domain. Moreover, Q is a prime ideal in S such that Q 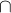 R = (0). Note that
we have shown above that there is a non-zero d in R such that Rd
R = (0). Note that
we have shown above that there is a non-zero d in R such that Rd  Sd is
finite.
In this context we would like to show that given any maximal ideal M in
R, the maximal ideal N in S that lies over it also contains Q. By what we
have proved above, Q is the unique minimal prime in S. Then N must contain
Q.
Sd is
finite.
In this context we would like to show that given any maximal ideal M in
R, the maximal ideal N in S that lies over it also contains Q. By what we
have proved above, Q is the unique minimal prime in S. Then N must contain
Q.
Now, let J be any ideal in S and I = f-1(J); clearly f-1(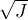 ) =
) = 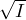 . Let P be a
minimal prime containing I then P contains the intersection of the prime ideals f-1(Q)
where Q runs over the minimal primes containing J; it thus equals one of them. Let M
be a maximal ideal in R that contains I. Then M contains a minimal prime ideal P for
I; let Q be the minimal prime containing J such that f-1(Q) = P. As shown above
N = f(M)S contains Q and this contains J as well. Hence we have shown that R
. Let P be a
minimal prime containing I then P contains the intersection of the prime ideals f-1(Q)
where Q runs over the minimal primes containing J; it thus equals one of them. Let M
be a maximal ideal in R that contains I. Then M contains a minimal prime ideal P for
I; let Q be the minimal prime containing J such that f-1(Q) = P. As shown above
N = f(M)S contains Q and this contains J as well. Hence we have shown that R  S is
closed.
S is
closed.
1.7. Conclusion. What we have shown above is that if R  S is a homomorphism of
finitely generated rings such that Hom(S,A)
S is a homomorphism of
finitely generated rings such that Hom(S,A)  Hom(R,A) is a bijection for all finite
rings A then R
Hom(R,A) is a bijection for all finite
rings A then R  S is closed. Now, consider the induced homomorphism R[X]
S is closed. Now, consider the induced homomorphism R[X]  S[X].
Since Hom(S[X],A) = Hom(S,A) ×A and Hom(R[X],A) = Hom(R,A) ×A we see that
Hom(S[X],A)
S[X].
Since Hom(S[X],A) = Hom(S,A) ×A and Hom(R[X],A) = Hom(R,A) ×A we see that
Hom(S[X],A)  Hom(R[X],A) is also a bijection. Then R[X]
Hom(R[X],A) is also a bijection. Then R[X]  S[X] is also
closed; this means that R
S[X] is also
closed; this means that R  S is finite as demonstrated earlier. Now S/R is a
finitely generated R-module such that (S/R)/M(S/R) = (0) for all maximal
ideals M in R. By Nakayama’s lemma we see that S/R = 0. We have already
seen that R
S is finite as demonstrated earlier. Now S/R is a
finitely generated R-module such that (S/R)/M(S/R) = (0) for all maximal
ideals M in R. By Nakayama’s lemma we see that S/R = 0. We have already
seen that R  S is injective. Thus it follows that R
S is injective. Thus it follows that R  S is an isomorphism as
required.
S is an isomorphism as
required.
 Y is a natural
transformation of functors such that the graph is a closed subscheme. Recall that a
natural transformation of functors on the category of finite rings gives a map
f(A) : X(A)
Y is a natural
transformation of functors such that the graph is a closed subscheme. Recall that a
natural transformation of functors on the category of finite rings gives a map
f(A) : X(A)  Y (A) for every finite ring A and for every morphism A
Y (A) for every finite ring A and for every morphism A  B the
following diagram commutes.
B the
following diagram commutes. 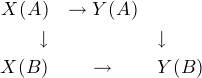
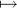
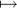
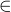
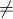 0 such that
0 such that 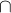
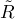 =
= 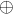
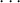 . Let
. Let 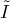 =
=  is a graded ideal in
is a graded ideal in 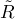 . In particular, it is finitely generated. Let
. In particular, it is finitely generated. Let 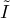 in terms of the generators, we conclude that
in terms of the generators, we conclude that
 (0). Let
(0). Let  ) =
) =  . Let
. Let