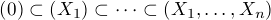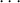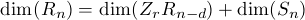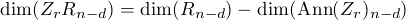DIMENSION THEORY
KAPIL HARI PARANJAPE
1. Dimension Theory
An affine variety associated with an Artinian ring should be said to have dimension 0
since there is nothing smaller that we consider in algebraic geometry. As we go to higher
dimensions we shall see below that there appear to be a number of different ways of
approaching the notion of dimension; luckily for us these all turn out to be the
same!
1.1. Chains of Prime ideals. If Spec(R) has dimension bigger than 0 then it should
have a proper subvariety; moreover we should ignore “nilpotent-thickenings” when
looking for subvarieties; for example, we should not consider Spec(k[X,Y ]/(Y )) to be a
proper subvariety of Spec(k[X,Y ]/(Y 2). From the point of view of components in the
sense introduced earlier, this easily translates into the notion of a proper subvariety
Spec(R/I) contained in Spec(R) as that associated with an ideal I such that none of the
minimal prime ideals containing I are minimal prime ideals of R. (We could also be a bit
more restrictive and insist that no associated prime of I should be an associated
prime for (0); but this works only for finitely generated rings R as we shall see
below.)
A sequence of varieties such that each is properly contained in the above sense
corresponds to a sequence I0 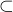 I1
I1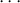 Ik such that the minimal primes containing Ir are
distinct from those that contain Ir+1. In particular we could take all the Ij’s to be
prime. The first definition of dimension p(R) of a ring is the maximum of the lengths of
strictly monotonic chains of prime ideals.
Ik such that the minimal primes containing Ir are
distinct from those that contain Ir+1. In particular we could take all the Ij’s to be
prime. The first definition of dimension p(R) of a ring is the maximum of the lengths of
strictly monotonic chains of prime ideals.
1.2. Complete Intersections. Any element of an Artinian ring is either a zero divisor
or is a unit. From this one would assume that a ring R has dimension bigger than 0 if
and only if we can find a function that is not a zero divisor or a unit. However, the
localisation of k[X,Y ]/(X2,XY ) at (X,Y ) has the property that every element of its
maximal ideal is a zero divisor--but the ring is not Artinian. Fortunately, this is not a
ring of the type we are considering--our rings are quotients of the polynomial ring in
finitely many variables (either over 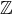 or over a field k). For such a ring R we can
define a complete intersection subvariety as one defined by a sequence (a1,...,ar)
where ak is not a zero divisor or unit in the ring R/(a1,...,ak-1). The dimension
s(R) can then be defined by considering the maximum over the length of such
sequences.
A relation of this to the previous definition can be understood by considering the
slightly larger class of all sequences (a1,...,ar) such that ak is not a zero divisor or unit
in the ring R/
or over a field k). For such a ring R we can
define a complete intersection subvariety as one defined by a sequence (a1,...,ar)
where ak is not a zero divisor or unit in the ring R/(a1,...,ak-1). The dimension
s(R) can then be defined by considering the maximum over the length of such
sequences.
A relation of this to the previous definition can be understood by considering the
slightly larger class of all sequences (a1,...,ar) such that ak is not a zero divisor or unit
in the ring R/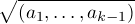 . Thus there is at least one prime ideal that contains
(a1,...,ak) that is not a minimal prime for (a1,...,ak-1). Let s0(R) denote the maximal
length of a sequence of this kind. Then s(R) < s0(R) < p(R).
. Thus there is at least one prime ideal that contains
(a1,...,ak) that is not a minimal prime for (a1,...,ak-1). Let s0(R) denote the maximal
length of a sequence of this kind. Then s(R) < s0(R) < p(R).
1.3. Finite morphisms. By definition the varieties Spec(R) that we are considering are
closed subvarietes of 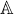 n for some n; such an inclusion can be identified with a surjective
homomorphism k[X1,...,Xn]
n for some n; such an inclusion can be identified with a surjective
homomorphism k[X1,...,Xn]  R Now, the dimension of
R Now, the dimension of 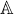 n ought to be n so that
dimension of R in this case ought to be less than n. How does one formalise this
approach to dimension.
First of all we need to expand from surjective homomorphisms to finite
homomorphisms. If R
n ought to be n so that
dimension of R in this case ought to be less than n. How does one formalise this
approach to dimension.
First of all we need to expand from surjective homomorphisms to finite
homomorphisms. If R  S is a finite ring homomorphism then each “point” of
Spec(R) has “finitely many” points of Spec(S) above it the following sense.
Let I be any ideal of R such that R/I is finite, then S/IS is also finite. Thus
we can see the dimension of S should be bounded above by the dimension of
R.
S is a finite ring homomorphism then each “point” of
Spec(R) has “finitely many” points of Spec(S) above it the following sense.
Let I be any ideal of R such that R/I is finite, then S/IS is also finite. Thus
we can see the dimension of S should be bounded above by the dimension of
R.
Let R  S be a finite homomorphism of rings and Q1
S be a finite homomorphism of rings and Q1 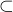 Q2 be a pair of distinct
primes in S. Replacing R by R/P1 and S by S/Q1, we have an injective finite
homomorphism of domains. The norm of a non-zero element a of S is a non-zero element
of aS
Q2 be a pair of distinct
primes in S. Replacing R by R/P1 and S by S/Q1, we have an injective finite
homomorphism of domains. The norm of a non-zero element a of S is a non-zero element
of aS 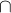 R. Thus f-1(Q2) is distinct from f-1(Q1).
R. Thus f-1(Q2) is distinct from f-1(Q1).
Now, if R  S is finite and injective and I is any ideal in R we have seen that IS
S is finite and injective and I is any ideal in R we have seen that IS 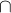 R
is contained in the radical of I. In particular, if P is prime then PS
R
is contained in the radical of I. In particular, if P is prime then PS 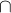 R = P. It
follows easily that there is a (minimal) prime ideal A containing PS such that
Q
R = P. It
follows easily that there is a (minimal) prime ideal A containing PS such that
Q 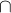 S = P.
S = P.
What we have shown is that for any finite morphism R  S we have p(R) > p(S) and
if in addition the morphism is injective then p(R) = p(S).
S we have p(R) > p(S) and
if in addition the morphism is injective then p(R) = p(S).
We can define the dimension f(R) of a ring R to be the smallest n such
that there is a finite ring homomorphism k[X1,...,Xn]  R. We then have
p(R) < p(k[X1,...,Xf(R)].
R. We then have
p(R) < p(k[X1,...,Xf(R)].
Thus, in order to prove that all the notions of dimensions coincide we need to show
that f(R) < s(R) and that the p dimension of the polynomial ring in n variables is in
fact n. We will first prove this by reformulating these notions for homogeneous
rings.
1.4. Homogeneous rings. Let us restrict our attention to homogeneous k-algebras R
where R0 = k. In this case the irrelevant ideal Irr(R) is a maximal ideal which contains
all homogeneous ideals. In the definitions above we should restrict our attention to
homogeneous ideals and homogeneous elements. We should also ignore the irrelevant
ideal(s).
We define P(R) to be the maximum length of a strictily monotic sequence of
homogeneous prime ideals in R none of which is the irrelevant ideal.
We define S0(R) to be the maximum length of a sequence a0, ..., an of
homogeneous elements of positive degree such that ak is not a zero-divisor in the ring
R/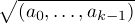 for any k.
for any k.
We define S(R) to be the maximum length of a sequence a1, ..., an of homogeneous
elements of positive degree such that for each k, ak is not a zero-divisor in the ring
R/((a0,...,ak-1) : Irr(R)s) for any s. Equivalently, if Rk denotes the ring R/(a0,...,ak),
then ak is not a zero-divisor in Rk-1/NRk-1, where NR denotes the “small” irrelevant
ideal of a graded ring R.
Finally, we define F(R) to be the smallest n for which there is a graded finite
homomorphism k[X0,...,Xn]  R.
R.
The above collection of inequalities remains valid for these definitions. We will now
establish a relation between F(R) and S(R).
1.5. Noether Normalisation. Let R be a finitely generated graded ring. Let us assume
that NR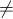 R or equivalently that there are associated primes of R that do not contain
the irrelevant ideal. Let P be a prime associated with the irrelevant ideal (this is just
the lift to R of an associated prime of (0) in R0). Then any P-primary ideal
contains a power of the irrelevant ideal and so P is not contained in any prime
associated with NR. Let aP be a homogeneous element of P that does not lie in any
associated prime of NR. The product a of the aP’s as P varies over the primes
associated with the irrelevant ideal is not in any associated prime of NR. On the
other hand some power of a lies in the irrelevant ideal. To conclude, there is a
homogeneous element of the irrelevant ideal that is not a zero-divisor modulo
NR.
We can go modulo such an element and iterate the process. This way we obtain a
sequence of elements z0, ..., zk such that if Rk = R/(z0,...,zk), then zk+1 is not a
zero-divisor in Rk/NRk. Since R is Noetherian we see that this process must
stop; at that stage Rk = NRk, or equivalently, the irrelevant ideal of Rk is
nilpotent.
R or equivalently that there are associated primes of R that do not contain
the irrelevant ideal. Let P be a prime associated with the irrelevant ideal (this is just
the lift to R of an associated prime of (0) in R0). Then any P-primary ideal
contains a power of the irrelevant ideal and so P is not contained in any prime
associated with NR. Let aP be a homogeneous element of P that does not lie in any
associated prime of NR. The product a of the aP’s as P varies over the primes
associated with the irrelevant ideal is not in any associated prime of NR. On the
other hand some power of a lies in the irrelevant ideal. To conclude, there is a
homogeneous element of the irrelevant ideal that is not a zero-divisor modulo
NR.
We can go modulo such an element and iterate the process. This way we obtain a
sequence of elements z0, ..., zk such that if Rk = R/(z0,...,zk), then zk+1 is not a
zero-divisor in Rk/NRk. Since R is Noetherian we see that this process must
stop; at that stage Rk = NRk, or equivalently, the irrelevant ideal of Rk is
nilpotent.
In particular, at that stage Rk is finite over R0. As we have seen earlier, this is
equivalent to the assertion that R is finite over the polynomial ring R0[Z0,...,Zk]. As a
consequence, we see that F(R) < S(R).
For future reference let us note that we could have started with any element z0 of the
irrelevant ideal which is not a zero-divisor in R/NR.
Finally, we need to show that the resulting homomorphism k[Z0,...,Zn]  R is
injective. We will prove this now.
R is
injective. We will prove this now.
1.6. All definitions are equal. For a graded k-algebra R with R0 = k we have
proved
![F(R) < S(R) < S0(R) < P (R) < P (k[X0,...,XF(R)]](dim4x.png)
Thus, all that remains is to prove that the p-dimension of a graded polynomial ring in
n + 1 variables is n. We will in addition prove that if z0,..., zr is a maximal sequence in
R as above then k[Z0,...,Zn]  R is injective as well.
R is injective as well.
This is clear for n = 0. Let us assume that we have proved the result for all smaller
dimensions. Let f be a non-zero homogeneous element of positive degree in
k[X0,...,Xn] and R = k[X0,...,Xn]/f. Since any minimal prime that contains (f) is
non-zero, we see that r = P(R) < P(k[X0,...,Xn]. By the induction hypothesis, we
have a graded inclusion k[Y 0,...,Y r]  R which is finite. We lift the images
of Y i to the polynomial ring and add f to this to obtain a homomorphism
k[Y 0,...,Y r+1]
R which is finite. We lift the images
of Y i to the polynomial ring and add f to this to obtain a homomorphism
k[Y 0,...,Y r+1]  k[X0,...,Xn] which is finite as well. Any element in the kernel of this
must go to 0 in R as well, but then it must be a multiple of Y r. Since f is not a
zero-divisor in the polynomial ring (being non-zero!) this is impossible. Thus, we
have a finite inclusion of one polynomial ring into another; by the theory of
transcendence we must have r + 1 = n. On the other hand we can choose any
homogeneous f of positive degree. Let (0
k[X0,...,Xn] which is finite as well. Any element in the kernel of this
must go to 0 in R as well, but then it must be a multiple of Y r. Since f is not a
zero-divisor in the polynomial ring (being non-zero!) this is impossible. Thus, we
have a finite inclusion of one polynomial ring into another; by the theory of
transcendence we must have r + 1 = n. On the other hand we can choose any
homogeneous f of positive degree. Let (0 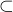 P1
P1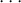 Ps be a maximal chain of
homogeneous prime ideals in k[X0,...,Xn] and f a non-zero element of P1. We see that
r = P(R) > s - 1 in this case. It follows that s < n and so P(k[X0,...,Xn]) < n as
required.
Ps be a maximal chain of
homogeneous prime ideals in k[X0,...,Xn] and f a non-zero element of P1. We see that
r = P(R) > s - 1 in this case. It follows that s < n and so P(k[X0,...,Xn]) < n as
required.
In the course of the proof we have proved two important facts that we also note. First
of all a single non-zero divisor in R/NR reduces the dimension by exactly 1. Secondly,
given a maximal sequence as in the definition of S(R) we obtain a graded inclusion
k[Z0,...,Zn]  R which is also finite; in particular, all such such sequences have length
equal to the dimension.
R which is also finite; in particular, all such such sequences have length
equal to the dimension.
1.7. Noether Normalisation for general rings. Let R be a finitely generated ring.
Expression R as a quotient of some polynomial ring we can define Rn as the elements of
degree at most n. Let Rh denote the corresponding homogenisation and T be the element
of Rh that represents 1 in R1. As proved earlier T is not a zero divisor in Rh
so NRh = 0. Thus we can find a maximal sequence z0 = T, z1, ...zn for Rh
which gives a finite inclusion k[Z0,...,Zn]  Rh. The ideal (Z0 - 1) is a radical
ideal in the polynomial ring and so (T - 1)
Rh. The ideal (Z0 - 1) is a radical
ideal in the polynomial ring and so (T - 1) 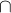 k[Z0,...,Zn] = (Z0 - 1). The
map
k[Z0,...,Zn] = (Z0 - 1). The
map
![h
k[Z0,...,Zn] = k[Z0,...,Zn]/(Z0- 1)-- > R = R /(T - 1)](dim6x.png)
is thus a finite inclusion. Thus we have produced a finite inclusion of a polynomial ring
into R as required.
1.8. Comparison of dimension for general rings. Now let R be any finitely
generated k-algebra. We have already shown that
![s(R) < s0(R) < p(R) < p(k[X1,...,Xf(R)]](dim7x.png)
Further, it is clear that if Rh is a homogenisation of R then p(R) < P(Rh) since a
sequence of prime ideals in P gives a sequence of homogeneous prime ideals in Rh which
are all distinct from the irrelevant ideal. Thus, we see that p(k[X1,...,Xn] < n. On the
other hand we have a natural sequence
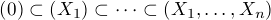
of prime ideals in the polynomial ring so p(k[X1,...,Xn] = n as required. We now only
need to show that f(R) < s(R).
Let a1,, ..., an be a maximal sequence in R as in the definition of s(R); then
R/(a1,...,an) consists of units and zero divisors. Let Rn be the homogenisation of R and
T be the element that corresponds to the element 1 in R1. We put zi = aiTdeg(ai) and
note that (z1,...,zi) is the homogenisation of the ideal (a1,...,ai). It follows that if
Rk = Rh/(z1,...,zk), then Rk is the homogenisation of R/(a1,...,ak). So NRk = 0, zk+1
is not a zero divisor in this ring and T is not a zero-divisor in Rn. In order to prove that
s(R) = S(Rh) it then suffices to show that Rn/T is finite. This is what we prove
next.
1.9. Hilbert’s Nullstellensatz. Let R be a finitely generated k-algebra which consists
only of units and zero-divisors. We claim that R is finite.
Any non-unit lies in an associated prime of (0) in R; let N denote the collection of
maximal elements among these. If M is a maximal ideal of R which is not in this
collection, then we can find an element of M which is not in any of the elements of N.
Such an element can not be a zero-divisor or a unit which contradicts the hypothesis. It
follows that R has finitely many maximal ideals.
We have seen above that there is a finite inclusion k[Z1,...,Zn]  R for some n; it is
enough to should that n = 0. Given finitely many non-constant polynomials f1,...fk,
the expression 1 + f1
R for some n; it is
enough to should that n = 0. Given finitely many non-constant polynomials f1,...fk,
the expression 1 + f1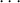 fk gives a non-constant polynomial which does not lie in any of
the ideals generated by a subset of the fi’s unless that sub-ideal is the full ring.
Thus, there are infinitely many maximal ideals in k[Z1]; it follows that there
are infinitely many maximal ideals in k[Z1,...,Zn] if n > 0. This proves the
result.
fk gives a non-constant polynomial which does not lie in any of
the ideals generated by a subset of the fi’s unless that sub-ideal is the full ring.
Thus, there are infinitely many maximal ideals in k[Z1]; it follows that there
are infinitely many maximal ideals in k[Z1,...,Zn] if n > 0. This proves the
result.
1.10. The Hilbert function. For a finitely generated graded ring R with R0 a finite
ring, the Hilbert function hR is defined by setting hR(n) to be the length of the Rn as an
R0 module. Let us concern ourselves with the case when R0 is a field k; the other case is
simlar. We claim that there is a polynomial PR(T) such that PR(n) = hR(n) for all n
sufficiently large; moreover, the degree of this polynomial is the graded dimenion of
R.
Let z0, ..., zr be a minimal system of homogeneous generators for a graded k-algebra
R as considered above. From what we have seen above, the resulting homomorphism
k[Z0,...,Zr]  R is finite and the dimension of R is also r. It follows that the
homomorphism is also injective.
R is finite and the dimension of R is also r. It follows that the
homomorphism is also injective.
We prove our assertion by induction on the dimension of R. When R is finite the
assertion is clear since hR(n) = 0 for n sufficiently large. Now suppose that Zr has degree
d and let S = R/(Zr). We see that
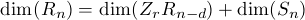
By induction we have a polynomial PS(T) of degree r - 1 such that dim(Sn) = PS(n)
for all sufficently large n. We also have
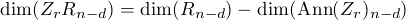
The ideal Ann(Zr) is a finitely generated module module over k[Z0,...,Zr-1] and so by
induction dim(Ann(Zr)n-d) is represented by a polynomial of degree at most r - 1. It
follows that we obtain (for all n sufficiently large) an identity hR(n) -hR(n-d) = Qr(n)
where Qr(T) is a polynomial of degree r. By “discrete integration” we observe that this
implies the result.
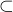 I1
I1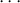 Ik such that the minimal primes containing Ir are
distinct from those that contain Ir+1. In particular we could take all the Ij’s to be
prime. The first definition of dimension p(R) of a ring is the maximum of the lengths of
strictly monotonic chains of prime ideals.
Ik such that the minimal primes containing Ir are
distinct from those that contain Ir+1. In particular we could take all the Ij’s to be
prime. The first definition of dimension p(R) of a ring is the maximum of the lengths of
strictly monotonic chains of prime ideals.
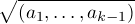 . Thus there is at least one prime ideal that contains
(
. Thus there is at least one prime ideal that contains
(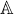

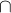
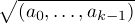 for any
for any 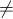
![F(R) < S(R) < S0(R) < P (R) < P (k[X0,...,XF(R)]](dim4x.png)
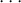
![h
k[Z0,...,Zn] = k[Z0,...,Zn]/(Z0- 1)-- > R = R /(T - 1)](dim6x.png)
![s(R) < s0(R) < p(R) < p(k[X1,...,Xf(R)]](dim7x.png)