The Asymmetric Top
We will ``approximate'' the asymmetric top by a finite set of point
masses which are attached to each other by massless, rigid rods
which ensure that the motion of the whole ensemble is described by a
path in the group of Euclidean motions in space. The exposition given
below is similar to that which can be found in the book on Classical
Mechanics by V. I. Arnold.
For the i-th point mass with mass mi, its position ri is a
function of time t given by the formula
ri(t) = g(t) . vi + r(t)
where vi is a constant vector and g is a path in the
orthogonal group. Let
M = 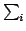 mi denote the total mass. The
position R of the centre of mass is given by
mi denote the total mass. The
position R of the centre of mass is given by
R =
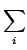 miri
miri/
M.
Moreover, if
V = 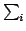 mivi/M, then we have
mivi/M, then we have
R(t) = g(t) . V + r(t).
If we set
ui = vi - V, then we obtain
We note that
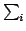 miui = 0.
miui = 0.
Now let us consider the velocity vectors of individual point masses,
Since g(t) is a path in the space of orthogonal matrices, we see that
g(t)-1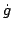 (t) is a skew-symmetric matrix. Hence there is a vector valued
function
(t) is a skew-symmetric matrix. Hence there is a vector valued
function
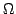 (t) so that for any vector u we have
(t) so that for any vector u we have
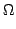
(
t)×
u =
g(
t)
-1 . 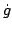
(
t)
. u
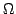 (t) is called the angular velocity about the centre of mass in the
body frame. If
(t) is called the angular velocity about the centre of mass in the
body frame. If
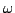 = g(t) .
= g(t) . 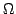 , then by applying g(t)
on all terms of the above equation, we see that for any vector r we have
, then by applying g(t)
on all terms of the above equation, we see that for any vector r we have
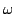
(
t)×
r =
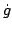
(
t)
. g(
t)
-1 . r
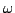 (t) is called the angular velocity about the centre of mass in the
stationary frame. Thus, we can re-write the velocity vector of the i-th
point mass
(t) is called the angular velocity about the centre of mass in the
stationary frame. Thus, we can re-write the velocity vector of the i-th
point mass
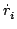
(
t) =
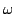
(
t)×(
ri -
R(
t)) +
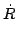
(
t)
The momentum of the system as a whole is given by
The angular momentum of the system as a whole in the stationary co-ordinates
is given by
(the remaining terms vanish because
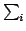 miri = MR). The latter term in the above expression for
miri = MR). The latter term in the above expression for
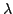 tot has the obvious interpretation as the
angular momentum of (a point mass concentrated at) the centre of
mass. The former term
tot has the obvious interpretation as the
angular momentum of (a point mass concentrated at) the centre of
mass. The former term
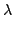
=
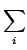 mi
mi(
ri -
R)×(
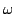
(
t)×(
ri -
R))
is referred to as the angular momentum of the system about
the centre of mass in the stationary frame. Applying g(t)-1 to the entire expression
gives
which is called the angular momentum in the body frame. We
note that the map
w 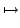 I
I(
w) =
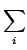 miui
miui×(
w×
ui)
depends only on the initial position of the point masses with respect
to their centre of mass and is thus associated to the configuration
or ``shape'' of this system; I is called the moment of
inertia or more strictly, the moment of inertia tensor of the
configuration of the point masses.
We can also compute the total kinetic energy
Ttot of the system
The latter term is the kinetic energy of a point mass concentrated at the
centre of mass. The former term
T =
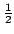
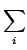 mi
mi||
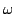
×(
ri -
R)||
2 =
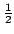
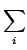 mi
mi||
×
ui||
2
is called the kinetic energy about the centre of mass or the
rotational kinetic energy. Note that
Using the identity
x.(y×z) = y.(z×x)
we obtain
x.I(w) = w.I(x); in other words I
is given by a symmetric matrix. We also see that
w.
I(
w) =
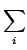 mi
mi||(
w×
ui)||
2 = ||
w||
2 mi
mi (distance of
ui from
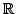 w
w)
2
Thus for a non-zero vector w, the latter quantity
Iw =
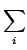 mi
mi (distance of
ui from
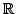 w
w)
2
is sometimes called the moment of inertia in the direction w;
it does not depend on the magnitude of w. Because I is
symmetric, there is an orthonormal eigen-basis
{e1,e2,e3} for I. The numbers
Ii = Iei are called the principal moments of the system.
The behaviour of the i-th point mass is dependent on the force
Fi acting on it. Newton's law states that
Fi = mi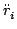 . From the expression for
. From the expression for
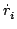 and the
identity
and the
identity
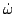 = g .
= g . 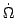 we obtain
we obtain
Let
F = 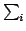 Fi. Then we have
F = M
Fi. Then we have
F = M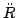 so
that the centre of mass of the system behaves as if the force F is
acting on (a point mass centred at) it. Now we compute the rate of
change of angular momentum,
so
that the centre of mass of the system behaves as if the force F is
acting on (a point mass centred at) it. Now we compute the rate of
change of angular momentum,
The former term is called the torque acting on the system
about the centre of mass in the stationary frame. If we split
Fi as
Gi + Hi, where Gi is towards
the centre of mass (i. e. parallel to the vector
ri - R) and Hi is orthogonal to it; then
clearly the torque is given by
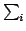 (ri - R)×Hi. As before we can apply
g(t)-1 to it to obtain
(ri - R)×Hi. As before we can apply
g(t)-1 to it to obtain
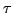 =
= 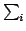 ui×hi as the torque acting on the top in the body frame; here
hi = g-1Hi. On the other hand, using the above
expression for
ui×hi as the torque acting on the top in the body frame; here
hi = g-1Hi. On the other hand, using the above
expression for
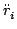 we see that
we see that
We apply g-1 to express everything in the body frame.
This expression in the body frame for the derivative of the angular
momentum in terms of the torque and the angular velocity is called
Euler's equation.
To summarise, the motion of an asymmetric top can separated into two
components, the motion of its centre of mass and the motion about the
centre of mass. The centre of mass behaves exactly like a point of mass
M with position R subject to a force F under
Newton's equations. The motion
about the centre of mass is described in the body frame by a path g
is the group of rotations, the moment of inertia tensor I and torque
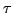 to which the body is subjected. The equation of motion in this
case is Euler's equation. Since the motion of a point mass in a
Newtonian system is well understood, we will concentrate on the latter.
to which the body is subjected. The equation of motion in this
case is Euler's equation. Since the motion of a point mass in a
Newtonian system is well understood, we will concentrate on the latter.
The only expression that depends on the distribution of masses is I.
Replacing the summation by integration and the masses by a mass density
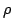 , we see that another expression for the moment of inertia is
, we see that another expression for the moment of inertia is
Similarly, we see that
where
d (r,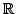 w) denotes the distance of r from
the line
w) denotes the distance of r from
the line
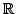 w. If we perform these computations for a
ellipsoid with principal axes being the co-ordinate axes with principal
lengths a, b and c, then
w. If we perform these computations for a
ellipsoid with principal axes being the co-ordinate axes with principal
lengths a, b and c, then
(x, y, z).I((x, y, z)) = const. . ((b2 + c2)x2(c2 + a2)y2(a2 + b2)z2)
In particular, note that the ``shape'' of the surface
w.I(w) = 1 is quite different from that of the boundary of
the given ellipsoid.
We say that the rotation is inertial if the torque vanishes;
i. e.
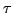 = 0.
It follows that
= 0.
It follows that
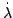 = 0 so that the angular
momentum
= 0 so that the angular
momentum
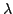 in the stationary frame is conserved. In
particular, the magnitude
||
in the stationary frame is conserved. In
particular, the magnitude
||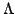 || = ||
|| = ||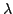 || of the
angular momentum in the body frame is preserved. Moreover, taking the
derivative of the rotational kinetic energy
T =
|| of the
angular momentum in the body frame is preserved. Moreover, taking the
derivative of the rotational kinetic energy
T = 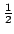
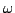 .
.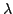 =
= 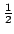
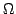 .
.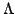 we see (using the symmetry of I) that
we see (using the symmetry of I) that
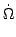
.
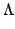
=
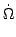
.
I(
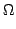
) = (
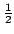
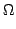
.
I(
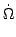
) +
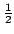
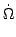
.
I(
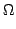
)) =
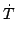
=
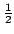
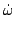
.
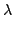
=
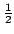
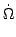
.
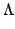
Thus
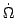 .
.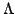 =
= 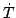 = 0 and the so kinetic
energy T in the body frame is preserved. It follows that
= 0 and the so kinetic
energy T in the body frame is preserved. It follows that
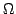 lies on the intersection of the sphere S defined by
||
lies on the intersection of the sphere S defined by
||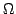 || = const. and the ellipsoid E
defined by
|| = const. and the ellipsoid E
defined by
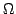 .I(
.I(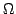 ) = const.; the ellipsoid
could be degenerate in case I is not invertible (but this won't happen
for ``solid'' tops).
) = const.; the ellipsoid
could be degenerate in case I is not invertible (but this won't happen
for ``solid'' tops).
Poinsot offered a more precise description as follows. Consider the
image g . E of the ellipsoid. The vector
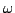 = g .
= g . 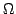 lies on this ellipsoid. Moreover, a
vector w is tangent to E at
lies on this ellipsoid. Moreover, a
vector w is tangent to E at
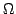 if
w.
if
w.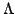 = w.I(
= w.I(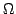 ) = 0. Thus a vector
x is tangent to g . E at
) = 0. Thus a vector
x is tangent to g . E at
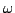 if
x.
if
x.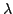 = 0. Said differently, the tangent plane
= 0. Said differently, the tangent plane 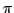 to
g . E at
to
g . E at
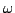 consists of vectors y such that
y.
consists of vectors y such that
y.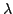 =
= 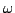 .
.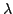 . We recognise the
latter expression as 2T, twice the rotational kinetic energy, which
is a constant of motion. In other words,
. We recognise the
latter expression as 2T, twice the rotational kinetic energy, which
is a constant of motion. In other words,  is also a constant of
motion.
is also a constant of
motion.
To summarise, the rotational motion g is such that the moving
ellipsoid g . E remains tangent to a fixed plane and the point of
tangency provides the axis of rotation; such a motion of the ellipsoid
E is called rolling without slipping on the plane  . To recover
the rotational motion of the original top we note that
(ri - R) = g . ui; so the top is ``affixed'' to the
ellipsoid through its centre of mass with the body frame aligned so
that the eigen-basis of the moment of inertia are the principal axes of
the ellipsoid. Warning: the reader should beware that we are not describing the inertial rotational motion of a top shaped like
E--rather the motion of E described gives a nice geometric
description of the motion of the original top.
. To recover
the rotational motion of the original top we note that
(ri - R) = g . ui; so the top is ``affixed'' to the
ellipsoid through its centre of mass with the body frame aligned so
that the eigen-basis of the moment of inertia are the principal axes of
the ellipsoid. Warning: the reader should beware that we are not describing the inertial rotational motion of a top shaped like
E--rather the motion of E described gives a nice geometric
description of the motion of the original top.
Kapil Hari Paranjape
2003-08-01
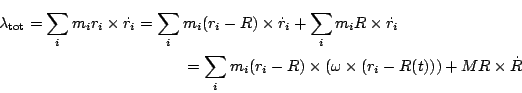
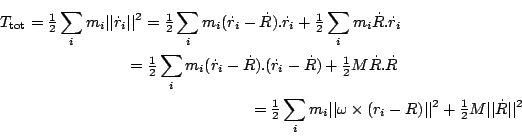
![]() . From the expression for
. From the expression for
![]() and the
identity
and the
identity
![]() = g .
= g . ![]() we obtain
we obtain
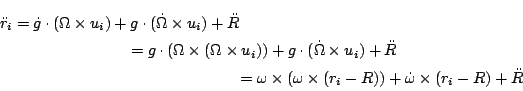
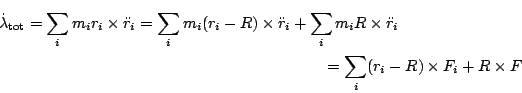
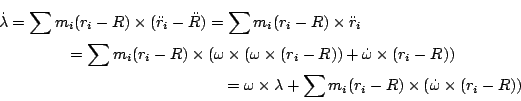
![]() to which the body is subjected. The equation of motion in this
case is Euler's equation. Since the motion of a point mass in a
Newtonian system is well understood, we will concentrate on the latter.
to which the body is subjected. The equation of motion in this
case is Euler's equation. Since the motion of a point mass in a
Newtonian system is well understood, we will concentrate on the latter.
![]() , we see that another expression for the moment of inertia is
, we see that another expression for the moment of inertia is
![]() = 0.
It follows that
= 0.
It follows that
![]() = 0 so that the angular
momentum
= 0 so that the angular
momentum
![]() in the stationary frame is conserved. In
particular, the magnitude
||
in the stationary frame is conserved. In
particular, the magnitude
||![]() || = ||
|| = ||![]() || of the
angular momentum in the body frame is preserved. Moreover, taking the
derivative of the rotational kinetic energy
T =
|| of the
angular momentum in the body frame is preserved. Moreover, taking the
derivative of the rotational kinetic energy
T = ![]()
![]() .
.![]() =
= ![]()
![]() .
.![]() we see (using the symmetry of I) that
we see (using the symmetry of I) that
![]() = g .
= g . ![]() lies on this ellipsoid. Moreover, a
vector w is tangent to E at
lies on this ellipsoid. Moreover, a
vector w is tangent to E at
![]() if
w.
if
w.![]() = w.I(
= w.I(![]() ) = 0. Thus a vector
x is tangent to g . E at
) = 0. Thus a vector
x is tangent to g . E at
![]() if
x.
if
x.![]() = 0. Said differently, the tangent plane
= 0. Said differently, the tangent plane ![]() to
g . E at
to
g . E at
![]() consists of vectors y such that
y.
consists of vectors y such that
y.![]() =
= ![]() .
.![]() . We recognise the
latter expression as 2T, twice the rotational kinetic energy, which
is a constant of motion. In other words,
. We recognise the
latter expression as 2T, twice the rotational kinetic energy, which
is a constant of motion. In other words, ![]() is also a constant of
motion.
is also a constant of
motion.
![]() . To recover
the rotational motion of the original top we note that
(ri - R) = g . ui; so the top is ``affixed'' to the
ellipsoid through its centre of mass with the body frame aligned so
that the eigen-basis of the moment of inertia are the principal axes of
the ellipsoid. Warning: the reader should beware that we are not describing the inertial rotational motion of a top shaped like
E--rather the motion of E described gives a nice geometric
description of the motion of the original top.
. To recover
the rotational motion of the original top we note that
(ri - R) = g . ui; so the top is ``affixed'' to the
ellipsoid through its centre of mass with the body frame aligned so
that the eigen-basis of the moment of inertia are the principal axes of
the ellipsoid. Warning: the reader should beware that we are not describing the inertial rotational motion of a top shaped like
E--rather the motion of E described gives a nice geometric
description of the motion of the original top.