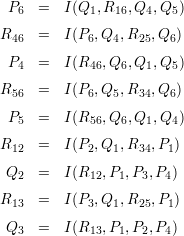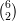 = 27
lines1 .
= 27
lines1 .
A double-six consists of a pair of ordered 6-tuples of lines (P0,…,P5) and (Q0,…,Q5) such that each Pi meets all the Qj except Qi.
For each i and j consider the intersection of the plane spanned by Pi and Qj with that spanned by
Pj and Qi; this gives a line Rij which meets all the four lines. This gives us 6 + 6 + 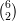 = 27
lines1 .
= 27
lines1 .
We will construct a Shlafly double-six and write the equation of the (unique) cubic that contains it.
Let F denote the smooth quadric in ℙ3 defined by XY - ZT = 0. This contains the lines:
This choice of lines means that Pi meets Qj for i = 1,2,3 and j = 4,5,6. At the same time the Pi’s are mutually disjoint; as are the Qj’s. Conversely, given such a collection of six lines we can always choose co-ordinates so that these lines are given by the equations above. As a consequence such a configuration always lies in a (unique) smooth quadric.
We take a general linear polynomial aT + bX + cY + dZ and consider the cubic surface S defined by the equation
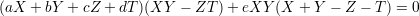
It is clear that the lines above are contained in S. Conversely, any cubic that contains the six lines defined above has this form.
We will construct the Shlafly double-six for S by suitably choosing the constants a, b, c, d, e. Now S also contains the lines:
We want a line Q1 which meets the lines P2, P3 and R16. Since the latter three are skew lines, Q1 is uniquely determined by its intersection with P2 as follows. Let us pick a point x21 of P2 given by (X : Y : Z : T) = (t : 0 : 1 : 0). Let π61 be the span of x21 and the line R16 and let π31 be the span of x21 and the line P3. Then Q1 is the line where the planes π61 and π31 intersect.
In order that S contains Q1 we need to choose the constants a, b, c, d and e so that
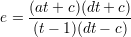
If this is done then the cubic S contains Q1. We claim that this cubic contains a Schlafly double-six which we now construct.
We will repeatedly apply the following construction. Let L1, L2, M1 and M2 be lines in S such that:
Let π be the plane containing L1 and L2. The intersection of S and π contains L1 and L2. The residual intersection is then another line L3. The intersection of Mi with the plane π does not lie on L1 or L2 and hence must lie on on L3. We can thus construct L3 as the line joining the intersection of M1 and π with the intersection of M2 and π. We denote this line by I(L1,L2,M1,M2).
The inductive construction of the remaining lines in the double-six is as follows: