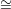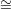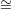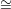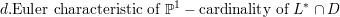LECTURE II
GENUS OF CURVES
KAPIL HARI PARANJAPE
A smooth projective curve C over a field k is by definition a smooth irreducible projective variety of
dimension 1 over k. To begin with let us think of C ⊂ ℙn for some unspecified n. We want to study intrinsic
properties of C; properties that are independent of the specific way in which it is expressed as closed
sub-variety of ℙn. The fundamental invariant associated with C is its genus g. The genus can be defined in
many different ways.
The arithmetic genus of C is defined as follows. Consider the homogeneous co-ordinate ring R of C; recall
that this is the quotient of the polynomial ring k[X0,…,Xn] (which is the homogeneous co-ordinate ring of
ℙn) by the (homogeneous) ideal generated by the equations defining C. The statement that C is of
dimension 1 is equivalent to the statement that there is a linear subspace L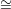 ℙn-2 of ℙn-2 which does not
meet C; moreover, the projection away from L gives a morphism X → ℙ1 which has finite fibres. After a
linear change of co-ordinates we may assume that L is defined by the vanishing of X0 and
X1. The algebraic version of the above statement about C is that the ring homomorphism
k[X0,X1] → R is injective and makes R a finitely generated graded module over k[X0,X1]. It follows
that the dimension of Rm is a linear function of m for sufficiently large m. Writing this linear
function as md + 1 - g, we note that d is the rank of R as a module over k[X0,X1] which is
geometrically described as the number of points in the general fibre of C → ℙ1; this is called the degree
of the curve C. The number g is called the “defect” or arithmetic genus of the curve C. Of
course, it needs to be shown that g is non-negative and is independent of the embedding of C in
ℙn.
ℙn-2 of ℙn-2 which does not
meet C; moreover, the projection away from L gives a morphism X → ℙ1 which has finite fibres. After a
linear change of co-ordinates we may assume that L is defined by the vanishing of X0 and
X1. The algebraic version of the above statement about C is that the ring homomorphism
k[X0,X1] → R is injective and makes R a finitely generated graded module over k[X0,X1]. It follows
that the dimension of Rm is a linear function of m for sufficiently large m. Writing this linear
function as md + 1 - g, we note that d is the rank of R as a module over k[X0,X1] which is
geometrically described as the number of points in the general fibre of C → ℙ1; this is called the degree
of the curve C. The number g is called the “defect” or arithmetic genus of the curve C. Of
course, it needs to be shown that g is non-negative and is independent of the embedding of C in
ℙn.
Another notion is that of the Todd genus of C. Let (ℙn)* be the dual projective space of ℙn
which we think of as the space parametrising hyperplanes (linear ℙn-1’s) in ℙn. Recall that this
is expressed by writing the correspondence I in ℙn × (ℙn)* which is defined by the equation
∑
iXiY i = 0 if Xi’ and Y i’s are homogeneous co-ordinates in ℙn and (ℙn)* respectively. Now,
consider the dual variety DC in (ℙn)*, which is the locus of all hyperplanes that are tangent to C.
More precisely, we can describe it as follows. For each point p in C, we have a line Tp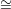 ℙ1
which is tangent to C at p. Consider the sub-variety J of I which is the locus of all pairs (p,H)
where p lies on C and H is a hyperplane in ℙn (and hence a point of (ℙn)*) that contains Tp.
Then DC is the image of J in (ℙn)*. If k is a field of characteristic zero or if we replace the
given embedding of C by a Veronese twist, then J → D is an isomorphism over an open subset
of DC. It follows that DC is of dimension n - 1 and is thus defined by a single homogeneous
polynomial F in the Y i’s. We write the degree of this polynomial as 2d + 2g - 2, where d is the
degree of C; equivalently the Todd genus of C is defined as (deg(F)∕2) + 1 - d. Of course, one
needs to show that this is a non-negative integer and independent of the embedding of C in
ℙn.
ℙ1
which is tangent to C at p. Consider the sub-variety J of I which is the locus of all pairs (p,H)
where p lies on C and H is a hyperplane in ℙn (and hence a point of (ℙn)*) that contains Tp.
Then DC is the image of J in (ℙn)*. If k is a field of characteristic zero or if we replace the
given embedding of C by a Veronese twist, then J → D is an isomorphism over an open subset
of DC. It follows that DC is of dimension n - 1 and is thus defined by a single homogeneous
polynomial F in the Y i’s. We write the degree of this polynomial as 2d + 2g - 2, where d is the
degree of C; equivalently the Todd genus of C is defined as (deg(F)∕2) + 1 - d. Of course, one
needs to show that this is a non-negative integer and independent of the embedding of C in
ℙn.
Assume that k is a field of characteristic 0. The coefficients of a given system of equations defining C
generate a sub-field E of k which is a finitely generated extension of ℚ, the field of rational numbers. Any
such field can be embedded in ℂ, the field of complex numbers. Choose such an embedding. With all these
choices, we can now take the “same” curve over the field of complex numbers. As seen in other lectures, this
gives a compact oriented topological manifold of (real) dimension 2. Such a manifold can be visualised as
a sphere with g handles for a certain non-negative integer g which is called the topological
genus. As before, one must show that this definition is independent of the various choices made
above.
How does one extend the above definition to fields of non-zero characteristic. We notice that the
abelianised fundamental group of C is the free abelian group on 2g generators. This motivates the following
definition. Let l be a prime number different from the characteristic of k; we also assume that k is separably
closed. Consider the isomorphism classes (over C) of finite smooth morphisms C′→ C which are Galois and
of degree l. The number of such classes is N = (l2g - 1)∕(l - 1). In other words the genus of C is the half of
the number of “digits” required to express N in base l. As before, we need to show that this number is
independent of the l chosen.
Now one way to prove that the various definitions of genus are independent of the choices made
is to show that they are equal! For example, it is clear the the topological definitions do not
depend on the embedding in ℙn and give non-negative integers. On the other hand it is clear
that the algebraic definitions are independent of any of the choices made in the topological
definitions.
Let Nd denote the rational normal curve of degree d in ℙd; it is the image of the d-tuple Veronese
embedding of ℙ1 in ℙd. Let d be much larger than g and let us choose g disjoint pairs (Pi,Qi) of distinct
points in Nd. Let L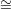 ℙ2g-1 be the linear span of these 2g points and Ai
ℙ2g-1 be the linear span of these 2g points and Ai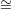 ℙ1 be the line that joins Pi with
Qi. Let M
ℙ1 be the line that joins Pi with
Qi. Let M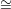 ℙg-1 be a linear space in L that meets each Ai at a point Ri that is distinct from Pi and
Qi. Let C0 be the image of Nd in ℙd-g under projection away from M. We note that (by the
non-vanishing of the Vandermonde determinant), L meets Nd precisely (and transversely) in the points
Pi’s and Qi’s. So C0 is obtained by identifying (or pinching together) the pairs of points on
Nd.
ℙg-1 be a linear space in L that meets each Ai at a point Ri that is distinct from Pi and
Qi. Let C0 be the image of Nd in ℙd-g under projection away from M. We note that (by the
non-vanishing of the Vandermonde determinant), L meets Nd precisely (and transversely) in the points
Pi’s and Qi’s. So C0 is obtained by identifying (or pinching together) the pairs of points on
Nd.
Let us put this more algebraically. The homogeneous co-ordinate ring R of Nd is the sub-ring of k[U,V ]
generated by all monomials UiV d-i of degree d; the assignment Ti UiV d-i gives a surjective
homomorphism k[T0,…,Td] → R. The line Ai corresponds to a rank-2 quotient Wi of the linear space
spanned by the Ti (the kernel of this map is the ideal defining Ai). The points Pi, Qi and Ri correspond to
distinct rank-1 quotients of Wi. It follows that we can think of Ri as the graph of an isomorphism between
the quotients corresponding to Pi and Qi. In other words, we obtain graded homomorphisms Pi : R → k[P]
and Qi : R → k[Q] and Ri is a graded isomorphism between k[P] and k[Q]. Then the co-ordinate ring S of
C0 is the sub-ring of R consisting of those elements F such that for each i the image of F
under Pi and Qi are identified under the isomorphism given by Ri. It is thus clear that the
rank of the graded piece Sm is precisely g less than the rank of the graded piece Rm. Since the
latter has rank precisely md + 1, it follows that C0 is a (singular) curve with arithmetic genus
g.
UiV d-i gives a surjective
homomorphism k[T0,…,Td] → R. The line Ai corresponds to a rank-2 quotient Wi of the linear space
spanned by the Ti (the kernel of this map is the ideal defining Ai). The points Pi, Qi and Ri correspond to
distinct rank-1 quotients of Wi. It follows that we can think of Ri as the graph of an isomorphism between
the quotients corresponding to Pi and Qi. In other words, we obtain graded homomorphisms Pi : R → k[P]
and Qi : R → k[Q] and Ri is a graded isomorphism between k[P] and k[Q]. Then the co-ordinate ring S of
C0 is the sub-ring of R consisting of those elements F such that for each i the image of F
under Pi and Qi are identified under the isomorphism given by Ri. It is thus clear that the
rank of the graded piece Sm is precisely g less than the rank of the graded piece Rm. Since the
latter has rank precisely md + 1, it follows that C0 is a (singular) curve with arithmetic genus
g.
Now, suppose we could show that as we “deform” C0 in ℙd-g, the singularities of C0 will disappear.
Moreover, suppose we could show that such deformations “reach” all curves of arithmetic genus g in ℙd-g.
These two statements can be proved by the use of Hilbert schemes (which were introduced in the previous
lecture). Assuming these results let us see why the topological genus of the curves so obtained is also
g.
How does one deform away the singularity of C0? To understand this let us see how one can obtain C0
from a smooth oriented compact manifold of (real) dimension 2. As noted above, such a manifold can be
visualised as a sphere with g handles. Let us choose a loop around each handle and collapse this loop to
a point. We see that we obtain a surface of the same topological (homeomorphism) type as
C0.
To understand the relation between the Todd genus and the topological genus, we note that a general line
L*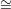 ℙ1 in (ℙn)* corresponds to a linear subspace L
ℙ1 in (ℙn)* corresponds to a linear subspace L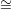 ℙn-2 in ℙn; each point of L corresponds to a
hyperplane in ℙn that contains L. Now, as we mentioned above, a general such L does not meet C and
projection away from L can be identified as a morphism f : X → L*; the fibre over a point
p in L* being the intersection of the corresponding hyperplane with C. As we saw earlier, f
has degree d. Now, the intersection of L* with the dual variety DC corresponds precisely to
those hyperplanes that meet C tangentially. For a general choice of L the intersection of DC
and L is transversal; this means that the hyperplane corresponding to this intersection has
exactly d - 1 points with tangency at one of these points. (This is called a Lefschetz pencil of
hyperplanes for the curve C). Let us choose a triangulation of L*
ℙn-2 in ℙn; each point of L corresponds to a
hyperplane in ℙn that contains L. Now, as we mentioned above, a general such L does not meet C and
projection away from L can be identified as a morphism f : X → L*; the fibre over a point
p in L* being the intersection of the corresponding hyperplane with C. As we saw earlier, f
has degree d. Now, the intersection of L* with the dual variety DC corresponds precisely to
those hyperplanes that meet C tangentially. For a general choice of L the intersection of DC
and L is transversal; this means that the hyperplane corresponding to this intersection has
exactly d - 1 points with tangency at one of these points. (This is called a Lefschetz pencil of
hyperplanes for the curve C). Let us choose a triangulation of L*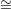 ℙ1 such that the points
of L*∩ D are vertices in this triangulation. We then see that the Euler characteristic of C
is
ℙ1 such that the points
of L*∩ D are vertices in this triangulation. We then see that the Euler characteristic of C
is
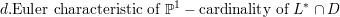
For a compact oriented manifold of (real) dimension 2, the Euler characteristic is 2 - 2g, thus we see that
the Todd genus and topological genus are the same.
The assertion that the Todd genus is the same as the arithmetic genus can be seen as the
principal assertion of the Riemann-Roch theorem for curves (which also asserts a bit more!). In
particular, Hirzebruch and Grothendieck were able to generalise much of the above through
their extension of the Riemann-Roch theorem. Numerous simpler proofs of this theorem have
been given since Hirzebruch and Grothendieck first published their proofs; notably one by V.
K. Patodi using differential geometry and one more recently by M. V. Nori which is purely
algebraic.
Let X ⊂ ℙn be a smooth projective variety and R be its homogeneous co-ordinate ring. Since this is a
finitely generated graded ring over k, the rank of Rm is a polynomial function of m for all sufficiently large
m. To express the coefficients of this polynomial in terms of certain intersection numbers like the degree of
X, the degree of the dual variety of X and so on is the consequence of these generalisations of the
Riemann-Roch theorem for curves. At the same time, such intersection numbers should be computable using
topological properties of X.
As an exercise compute the different genuses for a plane curve.
 ℙn-2 of ℙn-2 which does not
meet C; moreover, the projection away from L gives a morphism X → ℙ1 which has finite fibres. After a
linear change of co-ordinates we may assume that L is defined by the vanishing of X0 and
X1. The algebraic version of the above statement about C is that the ring homomorphism
k[X0,X1] → R is injective and makes R a finitely generated graded module over k[X0,X1]. It follows
that the dimension of Rm is a linear function of m for sufficiently large m. Writing this linear
function as md + 1 - g, we note that d is the rank of R as a module over k[X0,X1] which is
geometrically described as the number of points in the general fibre of C → ℙ1; this is called the degree
of the curve C. The number g is called the “defect” or arithmetic genus of the curve C. Of
course, it needs to be shown that g is non-negative and is independent of the embedding of C in
ℙn.
ℙn-2 of ℙn-2 which does not
meet C; moreover, the projection away from L gives a morphism X → ℙ1 which has finite fibres. After a
linear change of co-ordinates we may assume that L is defined by the vanishing of X0 and
X1. The algebraic version of the above statement about C is that the ring homomorphism
k[X0,X1] → R is injective and makes R a finitely generated graded module over k[X0,X1]. It follows
that the dimension of Rm is a linear function of m for sufficiently large m. Writing this linear
function as md + 1 - g, we note that d is the rank of R as a module over k[X0,X1] which is
geometrically described as the number of points in the general fibre of C → ℙ1; this is called the degree
of the curve C. The number g is called the “defect” or arithmetic genus of the curve C. Of
course, it needs to be shown that g is non-negative and is independent of the embedding of C in
ℙn.