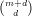A correspondence between a pair of algebraic varieties X and Y can loosely be defined as a closed sub-variety Z of the product X × Y . One obvious example is the graph Γ_f of a morphism f : X → Y . However, note that there is a natural symmetry which interchanges correspondences between X and Y with those between Y and X; the notion of morphism does not have such a symmetry.

The problem we shall consider today is how one can construct interesting correspondences. So perhaps an easier question could be how does one construct interesting morphisms. Since we are only considering quasi-projective varieties, a morphism X → Y can be thought of as a morphism X → ℙⁿ which happens to land inside the sub-variety Y ⊂ ℙⁿ. We have thus simplified the question; we now only ask how one constructs morphisms from X to ℙⁿ.

Since X is itself a sub-variety of ℙ^m for some m, we can try to construct morphisms from ℙ^m → ℙⁿ and go on from there. A fundamental example of such a morphism is the Veronese embedding ℙ^m → ℙ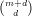^-1 given by

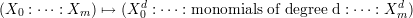
Another very important morphism is the projection ℙ^m \ ℙ^k → ℙ^m-k-1 given by

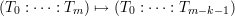
This morphism is cannot be extended along the sub-variety L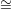ℙ^k ⊂ ℙ^m given by the equations T₀ = = T_m-k-1 = 0. In case our original variety X does not intersect L, then the morphism is defined on X. With an eye on the notion of correspondences we can consider the closure in ℙ^m × ℙ^m-k-1 of the graph B of the above morphism. We note that B → ℙ^m is an isomorphism over the open sub-variety ℙ^m \ L. The collection of all points in ℙ^m that are associated with a given (x₀ : : x_m-k-1) in ℙ^m-k-1 forms the linear subspace M_(x0::xm-k-1)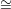ℙ^k+1 given by the equations x_jT_i = x_iT_j. It is clear that L ⊂ M_(x0::xm-k-1). In other words, we can think of B as the space of all pairs (p,M) where M is a linear subspace of dimension k + 1 in ℙ^m such that M contains L and the point p lies on M; when p is not in L, the linear span of p and L is M.

More generally, we can perform a “blow-up” of any X such that no component of X is contained in L. Consider the restriction of the projection morphism to X \L. We obtain a space B_X ⊂ X × ℙ^m-k-1 which is the closure of the graph of this morphism; this is called the blow-up of X along X ∩ L. The resulting correspondence is called a rational map on X.

The projection B_X → X is an isomorphism over the open sub-variety X \ (X ∩L). However, it could be an isomorphism on a bigger open sub-variety as well. In certain situations the first projection B_X → X is an isomorphism and then we obtain a morphism X → ℙ^m-k-1. It is an intriguing exercise to show that every morphism X → Y from a quasi-projective variety to another can be obtained by these means. In other words, given X ⊂ ℙ^m and Y ⊂ ℙⁿ and a morphism f : X → Y , there is a d and a linear subspace L in ℙ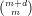^-1 such that the morphism f is obtained as the composition of the Veronese embedding X → ℙ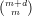^-1 with the projection from L, which is so chosen that B _X → X is an isomorphism.

An important example is the case when X is a smooth curve; by this we mean a smooth irreducible projective variety of dimension 1. Let p be a point of X and consider the projection from p. One can see that B_X is isomorphic to X; since there is “only one point missing” from X - p, the closure of this variety can only yield one more point! (Note the contrast between the algebraic context and the continuous context.) As an example, let us consider the curve in ℙ³ defined by the equations X² + Y ² = Z² and aX² + bY ² = W². Projecting this form a point on it gives a plane cubic curve in ℙ³. As an exercise you could try to write the equation of such a cubic.

Consider the variety B_ℙ^m in ℙ^m × ℙ^m-k-1 which is obtained as the graph of the rational map (projection) ℙ^m \ ℙ^k → ℙ^m-k-1. It is also useful to think of it as a correspondence from ℙ^m-k-1 to ℙ^m. As seen above it can be thought of as the family of all k + 1 dimensional linear spaces in ℙ^m that contain the fixed ℙ^k from which we are projecting. This naturally leads us the the question of whether we can find the family of all ℙ^k’s in ℙ^m.

For example, let us consider the sub-variety I of ℙⁿ × ℙⁿ defined by the equation ∑ X_iY _i = 0, where (X₀ : : X_n) and (Y ₀ : : Y _n) are the projective co-ordinates on the two ℙⁿ’s. For each point (a₀ : : a_n) of ℙⁿ, the equation ∑ a_iY _i = 0 defines a linear sub-space of dimension n - 1 in ℙⁿ. Conversely, any such linear space is defined by such an equation. Hence, we see that I can be thought of the variety parametrising such linear subspaces of dimension n - 1 — indeed, by symmetry this is true whichever way we look at this correspondence; with respect to the first factor or the second.

To take up a more asymmetric situation, let us consider the ℙ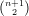^-1 whose projective co-ordinates we think of as tuples (X_ij) with the relations X_ii = 0 and X_ij + X_ji = 0. We then define the sub-variety I of ℙ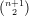^-1 × ℙⁿ by the equations X _ijY _k + X_jkY _i + X_kiY _j = 0 as i, j, k run over all possible values from 0 to n.

For each point (b₀ : : b_n) of ℙⁿ, the linear equations on the X_ij given by substituting b_i in place of Y _i give a linear subspace of ℙⁿ; it is an exercise to show that this is a linear space of dimension n - 1. (Hint: Try to show that if (x_ij) is a tuple satisfying these equations then x_ij = b_ic_j - b_jc_i for some c_i). The dimension of I is thus 2n- 1. One can similarly show that the linear space in ℙⁿ defined by the equations obtained on substituting X_ij by any tuple a_ij (such that a_ii = 0 and a_ij + a_ji = 0) is of dimension 1 if it is non-empty.

It follows that the image of I in ℙ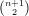^-1 is a variety of dimension 2n - 2; this is the Grassmannian variety 𝔾(1,n). Plücker did the necessary elimination theory to write down the explicit equations for this variety and so can you! One can generalise this approach to construct the Grassmannian variety 𝔾(k,n) which parametrises ℙ^k’s in ℙⁿ. The study of the geometry of the Grassmannian varieties (and other similar varieties) has attracted numerous algebraic geometers including C. S. Seshadri, C. Musili, V. Lakshmibai, A. Ramanathan, K. N. Raghavan and P. Sankaran.

More generally, suppose one is trying to parametrise all sub-varieties of “type” X in projective space ℙⁿ. If the homogeneous co-ordinate ring of X is R_X, one can say that Y has the same type as X if the graded components satisfy dim(R_Y )_m = dim(R_X)_m for all sufficiently large m. One can find a degree d so that X is defined by equations of degree d. Consider the d-tuple Veronese embedding of ℙⁿ in ℙ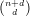^-1; denote the image by P _d. The sub-variety X in P_d is defined by linear equations and is thus given by the intersection of P_d with a suitable linear space ℙ^k in the ambient projective space. It is natural to expect (though it requires some effort to prove) that other sub-varieties in ℙⁿ of the same type as X are also obtained by intersecting P_d with linear subspaces of the same dimension; in other words, every Y with the property given above is also defined by same number of equations of degree d. However, it is unlikely (give an example!) that all linear spaces of dimension k will intersect P_d in a variety of type X. The condition that fixes the type will be a closed condition in the sense that there is a closed sub-variety of 𝔾(k,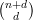- 1) for which the type will be preserved. This variety parametrises sub-varieties in P_d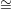ℙⁿ of the same type as X and is called the Hilbert scheme of subvarieties of type X in ℙⁿ. One can similarly construct Hilbert schemes of sub-varieties of a general projective variety Y . The natural incidence between the Hilbert scheme and Y gives an example of a very interesting correspondence.

To conclude this discussion let us take a simple example of the Hilbert scheme—the space of conics in ℙ². Consider the sub-variety of ℙ² × ℙ⁵ given by the equation

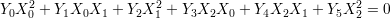
This exhibits ℙ⁵ as the space of conics in ℙ².