


Next: 11.3 Pohlig-Helman factor method
Up: 11 Algorithms for groups
Previous: 11.1 Pollard's
Now suppose that we know that we are given bounds L1, L2, ...
Lr with the assurance that there is a relation
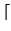 qiai
with
0
qiai
with
0 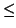 ai < Li. (We will see below how such a collection of
bounds can be constructed inductively given a bound L on the order
of G).
ai < Li. (We will see below how such a collection of
bounds can be constructed inductively given a bound L on the order
of G).
Let h(x) be a collision free function for x 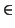 G (for example h
is a ``hash function''). Let
(a1,..., ar) be a sequence with
ai an integer not larger than
ni =
G (for example h
is a ``hash function''). Let
(a1,..., ar) be a sequence with
ai an integer not larger than
ni = 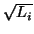
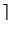
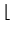 . We
compute the terms
. We
compute the terms
(
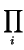 giai
giai;
a1,...,
ar;
h(
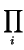 giai
giai))
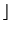
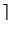
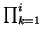 + 1, we compute the expression
h(
+ 1, we compute the expression
h(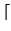 (gi-ni)bi) and try to find it in the given sorted
list. Clearly, if it is found then we have a relation of the form
(gi-ni)bi) and try to find it in the given sorted
list. Clearly, if it is found then we have a relation of the form
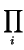 giai + nibi
giai + nibi = 1
By the given assertion on Li, such relation will eventually be
found.
One way to approach this algorithm given only a bound on the size of
the group G is to go inductively. First find a relation involving
g1 alone (in other words find the order of g1) by using L1 = L.
For the remainder of the algorithm we put
L1 = o(g1) as found in
this step. In the second iteration we work with g1 and g2 with
L2 = L/L1. Iteratively, we would have computed Li which is the
order of gi in the group
G/ < g1,..., gi - 1 >. We now work with
g1, ..., gi + 1 and take
Li + 1 = L/(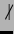 Li).
Using the above algorithm we obtain the order of gi + 1 in the
group
G/ < g1,..., gi >. For the remainder of the iterations we take
Li + 1 to be this order. Thus, at the end we would have found a
minimal relation among the gi's rather than just one
relation.
Li).
Using the above algorithm we obtain the order of gi + 1 in the
group
G/ < g1,..., gi >. For the remainder of the iterations we take
Li + 1 to be this order. Thus, at the end we would have found a
minimal relation among the gi's rather than just one
relation.



Next: 11.3 Pohlig-Helman factor method
Up: 11 Algorithms for groups
Previous: 11.1 Pollard's
Kapil Hari Paranjape
2002-10-20
![]() G (for example h
is a ``hash function''). Let
(a1,..., ar) be a sequence with
ai an integer not larger than
ni =
G (for example h
is a ``hash function''). Let
(a1,..., ar) be a sequence with
ai an integer not larger than
ni = ![]()
![]()
![]() . We
compute the terms
. We
compute the terms
![]() Li).
Using the above algorithm we obtain the order of gi + 1 in the
group
G/ < g1,..., gi >. For the remainder of the iterations we take
Li + 1 to be this order. Thus, at the end we would have found a
minimal relation among the gi's rather than just one
relation.
Li).
Using the above algorithm we obtain the order of gi + 1 in the
group
G/ < g1,..., gi >. For the remainder of the iterations we take
Li + 1 to be this order. Thus, at the end we would have found a
minimal relation among the gi's rather than just one
relation.